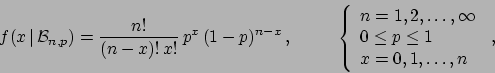 |
(1) |
| (2) | |||
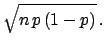 |
(3) |
The binomial distribution describes what is sometimes called
a direct probability problem, i.e. calculate
the probability of the experimental outcome ![]() (the effect)
given
(the effect)
given ![]() and an assumed value of
and an assumed value of ![]() . The inverse
problem is what concerns mostly scientists: infer
. The inverse
problem is what concerns mostly scientists: infer ![]() given
given
![]() and
and ![]() . In probabilistic terms, we are
interested in
. In probabilistic terms, we are
interested in ![]() .
Probability inversions
are performed, within probability theory, using Bayes theorem,
that in this case reads
.
Probability inversions
are performed, within probability theory, using Bayes theorem,
that in this case reads
The problem can be complicated by the presence of background. This is the main subject of this paper, and we shall focus on two kinds of background.
The problem will be solved assuming that the background is described
by a Poisson process of well known intensity ![]() , that corresponds
to a well known expected value
, that corresponds
to a well known expected value ![]() of the resulting
Poisson distribution (in the time domain
of the resulting
Poisson distribution (in the time domain
![]() ,
where
,
where ![]() is measuring time).
In other words, the observed
is measuring time).
In other words, the observed ![]() is the sum of two contributions:
is the sum of two contributions:
![]() due to the signal, binomially distributed with
due to the signal, binomially distributed with
![]() , plus
, plus ![]() due to background, Poisson
distributed with parameter
due to background, Poisson
distributed with parameter ![]() , indicated by
, indicated by
![]() .
.
For large numbers (and still relatively low background)
the problem is easy to solve: we subtract the expected number
of background and calculate the proportion
![]() .
For small numbers, the `estimator'
.
For small numbers, the `estimator' ![]() can become smaller
than 0 or larger then 1. And, even if
can become smaller
than 0 or larger then 1. And, even if ![]() comes out in the correct
range, it is still affected by large uncertainty. Therefore
we have to go through
a rigorous probability inversion, that in this case is given by
comes out in the correct
range, it is still affected by large uncertainty. Therefore
we have to go through
a rigorous probability inversion, that in this case is given by
| (5) |
| (6) | |||
| (7) |
| (8) | |||
| (9) | |||
| (10) |
Again, the trivial large number (and not too large background)
solution is the proportion
of background subtracted numbers,
![]() .
But in the most general case we need to infer
.
But in the most general case we need to infer ![]() from
from
| (11) |