


Next: Meaning and role of
Up: Inferring the success parameter
Previous: The binomial distribution and
Inferring 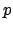 in absence of background
in absence of background
The solution of Eq.(4) depends, at least
in principle, on the assumption on the prior 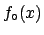 .
Taking a flat prior between 0 and 1, that models our
indifference on the possible values of
.
Taking a flat prior between 0 and 1, that models our
indifference on the possible values of 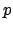 before
we take into account the result of the experiment in which
before
we take into account the result of the experiment in which
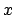 successes were observed in
successes were observed in 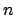 trials, we get
(see e.g. [2]):
trials, we get
(see e.g. [2]):
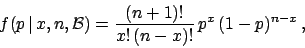 |
(12) |
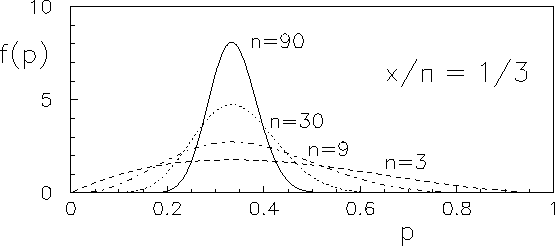
some examples of which are shown in Fig. 1.
Figure:
Probability density function of the binomial parameter
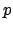 , having observed
, having observed 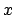 successes in
successes in 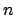 trials.[2]
trials.[2]
 |
Expected value, mode (the value of 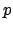 for which
for which 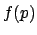 has the maximum) and variance of this distribution are:
has the maximum) and variance of this distribution are:
Eq. (13)
is known as
``recursive Laplace formula'',
or ``Laplace's rule of succession''.
Not that there is no magic if the formula
gives a sensible result even
for the extreme cases 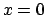 and
and 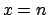 for all values of
for all values of 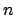 (even if
(even if 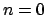 !).
It is just a consequence of the prior: in absence of new information,
we get out what we put in!
!).
It is just a consequence of the prior: in absence of new information,
we get out what we put in!
From Fig. 1 we can see that for large numbers
(and with 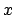 far from 0 and from
far from 0 and from 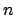 )
)
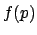 tends to a Gaussian. This is just the reflex of the limit
to Gaussian of the binomial. In this large numbers limit
tends to a Gaussian. This is just the reflex of the limit
to Gaussian of the binomial. In this large numbers limit
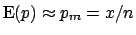 and
and
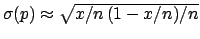 .
.
Subsections



Next: Meaning and role of
Up: Inferring the success parameter
Previous: The binomial distribution and
Giulio D'Agostini
2004-12-13

![]() far from 0 and from
far from 0 and from ![]() )
)
![]() tends to a Gaussian. This is just the reflex of the limit
to Gaussian of the binomial. In this large numbers limit
tends to a Gaussian. This is just the reflex of the limit
to Gaussian of the binomial. In this large numbers limit
![]() and
and
![]() .
.