Distribution of the ratio of Poisson $\lambda$'s by sampling

Once we have learned that the pdf of $\lambda$, in the light of the observation of $x$ count and assuming a flat prior, is a Gamma distribution, the easiest way to evaluate the distribution of $\lambda_1/\lambda_2$, for $x_2>0$, is by sampling. For example, using the following lines of R code,

x1 = 1
x2 = 1
lambda1 = rgamma(n, x1+1, 1)
lambda2 = rgamma(n, x2+1, 1)
rho = lambda1/lambda2

Then, varying x1 and x2 we can get the plots of Figs.  and .¹⁰

Figure: Estimate by sampling ( $n\!=\!10^7$) of $f(\rho_\lambda\!=\!\lambda_1/\lambda_2)$ for some `observed' counts. (For the (non) meaning of standard deviation for $x_1=x_2=1$ see Sec. .)

Figure: As Fig.  for larger values of the `observed' counts.

We immediately observe that the histograms are very regular, without divergences, although for small values of $x_2$ there is quite a long tail up to infinity, which is however reached with vanishing probability (the figures report also the proportions of overflows, having chosen the horizontal scale of the plots in order to show the most interesting part of each probability distribution). The mean and standard deviation (`std') shown on each plot are calculated from the Monte Carlo samples.

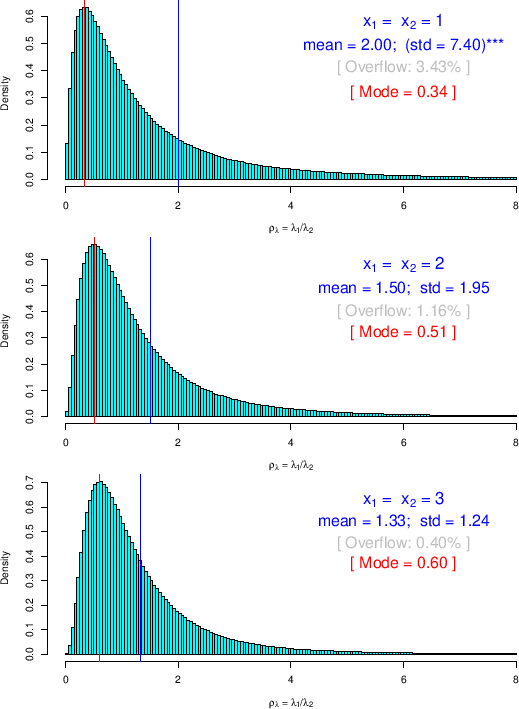The effect of the long tails is that there is quite a big difference between mean value and the most probable one, located around the highest bar of the histogram. This is not a surprise (the famous exponential distribution has modal value equal to zero independently of its parameter!), but it should sound as a warning for those who use analysis methods which provide, as `estimator', “the most probable value”¹¹ [13]. Moreover, for very small $x_2$ the tails do not seem to go very fast to zero (in comparison e.g. to the exponential), leading to not-defined moments of the distribution (of the theoretical one, obviously, since in most cases mean and standard deviation of the Monte Carlo distribution have finite values). This question will be investigated in the next subsection, after the derivation of closed expressions.

When $x_1$ and $x_2$ become `quite large' the Gamma distribution tends (slowly - think to the $\chi^2$, that is indeed a particular Gamma, as reminded in Appendix A) to a Gaussian, and likewise does (a bit slower) the ratio of two Gamma variables (as $\lambda_1$ and $\lambda_2$ are), as we can see for the case $x_1\!=\!x_2\!=\!100$ of Fig. ,¹²in which some skewness is still visible and the mode is about $3\%$ smaller than the mean value.