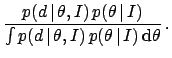Bayesian inference on uncertain variables and posterior characterization

We start here with a few one-dimensional problems involving simple models that often occur in data analysis. These examples will be used to illustrate some of the most important Bayesian concepts. Let us first introduce briefly the structure of the Bayes' theorem in the form convenient to our purpose, as a straightforward extension of what was seen in Sect. 4.2.

$$p(\theta\,\vert\,d,I) = \frac{p(d\,\vert\,\theta,I)\,p(\theta\,\vert\,I)} {\int p(d\,\vert\,\theta,I)\,p(\theta\,\vert\,I)\,\mbox{d}\theta}\,.$$ (24)

$\theta$ is the generic name of the parameter (used hereafter, unless the models have traditional symbols for their parameters) and $d$ is the data point. $p(\theta\,\vert\,I)$ is the prior, $p(\theta\,\vert\,d,I)$ the posterior and $p(d\,\vert\,\theta,I)$ the likelihood. Also in this case the likelihood is is often written as ${\cal L}(\theta; d) = p(d\,\vert\,\theta,I)$, and the same words of caution expressed in Sect. 4.2 apply here too. Note, moreover, that, while $p(d\,\vert\,\theta,I)$ is a properly normalized pdf, ${\cal L}(\theta; d)$ has not a pdf meaning in the variable $\theta$. Hence, the integral of ${\cal L}(\theta; d)$ over $\theta$ is only accidentally equal to unity. The denominator in the r.h.s. of Eq. (24) is called the evidence and, while in the parametric inference discussed here is just a trivial normalization factor, its value becomes important for model comparison (see Sect. 7).

Posterior probability distributions provide the full description of our state of knowledge about the value of the quantity. In fact, they allow to calculate all probability intervals of interest. Such intervals are also called credible intervals (at a specified level of probability, for example 95%) or confidence intervals (at a specified level of 'confidence', i.e. of probability). However, the latter expression could be confused with frequentistic 'confidence intervals', that are not probabilistic statements about uncertain variables (D'Agostini 1999c).

It is often desirable to characterize the distribution in terms of a few numbers. For example, mean value (arithmetic average) of the posterior, or its most probable value (the mode) of the posterior, also known as the maximum a posteriori (MAP) estimate. The spread of the distribution is often described in terms of its standard deviation (square root of the variance). It is useful to associate the terms mean value and standard deviation with the more inferential terms expected value, or simply expectation (value), indicated by $\mbox{E}(\,)$, and standard uncertainty (ISO 1993), indicated by $\sigma(\,)$, where the argument is the uncertain variable of interest. This will be our standard way of reporting the result of inference in a quantitative way, though, we emphasize that the full answer is given by the posterior distribution, and reporting only these summaries in case of the complex distributions (e.g. multimodal and/or asymmetrical pdf's) can be misleading, because people tend to think of a Gaussian model if no further information is provided.