 |
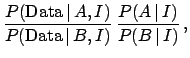 |
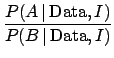
(88) |
We have seen so far two typical inferential situations:
| (92) |
| (93) |
This intuitive reasoning
is expressed formally in Eqs. (90) and (91).
The evidence is given integrating the product
![]() and
and
![]() over
the parameter space. So, the more
over
the parameter space. So, the more
![]() is concentrated around
is concentrated around
![]() ,
the greater is the evidence in favor of that model. Instead,
a model with a volume of the parameter space much larger
than the one selected by
,
the greater is the evidence in favor of that model. Instead,
a model with a volume of the parameter space much larger
than the one selected by
![]() gets disfavored.
The extreme limit is that of a hypothetical model with so many
parameters to describe whatever we shall observe.
This effect is very welcome, and follows the Ockham's Razor
scientific rule of discarding unnecessarily complicated models
(``entities should not be multiplied unnecessarily'').
This rule comes out of the Bayesian approach automatically
and it is discussed, with examples of applications
in many papers.
Berger and Jefferys (1992)
introduce the connection between Ockham's Razor and Bayesian
reasoning, and discuss the evidence provided by the motion
of Mercury's perihelion in favor of Einstein's general relativity theory,
compared to alternatives at that time. Examples of recent applications are
Loredo and Lamb 2002 (analysis of neutrinos observed from
supernova SN 1987A),
John and Narlikar 2002 (comparisons of cosmological models),
Hobson et al 2002
(combination of cosmological datasets)
and Astone et al 2003 (analysis of
coincidence data from gravitational wave detectors).
These papers also give
a concise account of underlying Bayesian ideas.
gets disfavored.
The extreme limit is that of a hypothetical model with so many
parameters to describe whatever we shall observe.
This effect is very welcome, and follows the Ockham's Razor
scientific rule of discarding unnecessarily complicated models
(``entities should not be multiplied unnecessarily'').
This rule comes out of the Bayesian approach automatically
and it is discussed, with examples of applications
in many papers.
Berger and Jefferys (1992)
introduce the connection between Ockham's Razor and Bayesian
reasoning, and discuss the evidence provided by the motion
of Mercury's perihelion in favor of Einstein's general relativity theory,
compared to alternatives at that time. Examples of recent applications are
Loredo and Lamb 2002 (analysis of neutrinos observed from
supernova SN 1987A),
John and Narlikar 2002 (comparisons of cosmological models),
Hobson et al 2002
(combination of cosmological datasets)
and Astone et al 2003 (analysis of
coincidence data from gravitational wave detectors).
These papers also give
a concise account of underlying Bayesian ideas.
After having emphasized the merits of model comparison
formalized in Eqs. (90) and (91),
it is important to mention a related problem.
In parametric inference we have seen that we can make an
easy use of improper priors
(see Tab. 1), seen as limits of proper priors, essentially
because they simplify in the Bayes formula. For example,
we considered
![]() of Eq. (26)
to be a constant, but this constant goes to zero as the
range of
of Eq. (26)
to be a constant, but this constant goes to zero as the
range of ![]() diverges. Therefore, it does simplify in
Eq. (26), but not, in general, in
Eqs. (90) and (91), unless
models
diverges. Therefore, it does simplify in
Eq. (26), but not, in general, in
Eqs. (90) and (91), unless
models ![]() and
and ![]() depend on the same number of parameters
defined in the same ranges. Therefore, the general case
of model comparison is limited to proper priors, and needs
to be thought through better than when making
parametric inference.
depend on the same number of parameters
defined in the same ranges. Therefore, the general case
of model comparison is limited to proper priors, and needs
to be thought through better than when making
parametric inference.