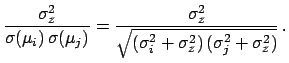Next: Approximate methods and standard
Up: Uncertainties from systematic effects
Previous: Joint inference and marginalization
We can easily extend Eqs. (73),
(77), and (79)
to a joint inference of several variables, which, as we
have seen, are nothing but parameters
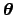 of suitable models. Using the alternative ways described in
Sects. 6.1 and 6.2, we have
of suitable models. Using the alternative ways described in
Sects. 6.1 and 6.2, we have
and
respectively. The two ways lead to an identical result, as it can be seen
comparing Eqs. (81) and (83).
Take a simple case of a common offset error
of an instrument used to measure various quantities 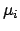 ,
resulting in the measurements
,
resulting in the measurements 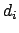 . We model each measurement as
. We model each measurement as 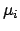 plus an error that is Gaussian distributed with a mean of zero and
a standard deviation
plus an error that is Gaussian distributed with a mean of zero and
a standard deviation 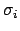 . The
calculation of the posterior distribution can be performed analytically,
with the following results (see D'Agostini 1999c for details):
. The
calculation of the posterior distribution can be performed analytically,
with the following results (see D'Agostini 1999c for details):
- The uncertainty in each
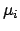 is described by a Gaussian centered
at
is described by a Gaussian centered
at 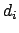 , with standard deviation
, with standard deviation
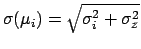 ,
consistent with Eq. (76).
,
consistent with Eq. (76).
- The joint posterior distribution
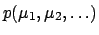 does not factorize
into the product of
does not factorize
into the product of 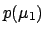 ,
, 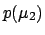 , etc., because correlations are
automatically introduced by the formalism, consistent with the
intuitive thinking of what a common systematic should do.
Therefore, the joint distribution will be a multi-variate Gaussian that
takes into account correlation terms.
, etc., because correlations are
automatically introduced by the formalism, consistent with the
intuitive thinking of what a common systematic should do.
Therefore, the joint distribution will be a multi-variate Gaussian that
takes into account correlation terms.
- The correlation coefficient between any pair
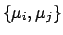 is given by
is given by
We see that
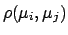 has the behavior expected from a
common offset error; it is non-negative; it varies from
practically zero, indicating negligible correlation, when
(
has the behavior expected from a
common offset error; it is non-negative; it varies from
practically zero, indicating negligible correlation, when
(
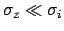 ), to unity (
), to unity (
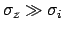 ),
when the offset error dominates.
),
when the offset error dominates.



Next: Approximate methods and standard
Up: Uncertainties from systematic effects
Previous: Joint inference and marginalization
Giulio D'Agostini
2003-05-13
![]() of suitable models. Using the alternative ways described in
Sects. 6.1 and 6.2, we have
of suitable models. Using the alternative ways described in
Sects. 6.1 and 6.2, we have
![]() ,
resulting in the measurements
,
resulting in the measurements ![]() . We model each measurement as
. We model each measurement as ![]() plus an error that is Gaussian distributed with a mean of zero and
a standard deviation
plus an error that is Gaussian distributed with a mean of zero and
a standard deviation ![]() . The
calculation of the posterior distribution can be performed analytically,
with the following results (see D'Agostini 1999c for details):
. The
calculation of the posterior distribution can be performed analytically,
with the following results (see D'Agostini 1999c for details):