



Next: Sintesi di una distribuzione
Up: Variabili casuali e distribuzioni
Previous: Combinazione di molti processi
Indice
Trattiamo prima la distribuzione geometrica, con un esempio che mette
in luce alcuni aspetti intuitivi e altri aspetti controintuitivi
legati alle distribuzioni di probabilità.
- Esempio
- Un ubriaco deve aprire la porta di casa al buio e
ha un mazzo di 8 chiavi ``indistinguibili''
(o che sembrano tali a lui).
Ammettiamo che, nel caso che egli non ci riesca in un tentativo,
la concitazione
e lo stato di annebbiamento gli impediscano di ricordare
con quale chiave abbia provato e quindi si ritrovi nelle stesse condizioni
nel tentativo successivo.
Cerchiamo di rispondere
a queste domande:
- -
- quanti tentativi si prevede che gli serviranno affinché riesca ad aprire
la porta?
- -
- se si dovesse fare una scommessa alla pari per vincere (``non coerente'')
su quale tentativo bisognerebbe puntare?
- Esempi analoghi
- Altri esempi schematizzabili nello stesso modo
sono: la prima volta che viene testa nel lancio di una moneta (
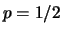 );
la prima volta che esce il 5 lanciando un dado (
);
la prima volta che esce il 5 lanciando un dado (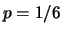 ) e la prima volta che
esce un numero su una certa ruota
del lotto (
) e la prima volta che
esce un numero su una certa ruota
del lotto (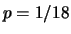 ).
).
È importante a confrontare fra loro i problemi
appena proposti prima di provare a rispondere intuitivamente
alle domande formulate a proposito
del problema dell'ubriaco. Le risposte intuitive
possono essere del tipo:
- ``passando, in ordine, dal problema della moneta
per terminare a quello del lotto,
bisogna considerare più tentativi prima di
sperare ragionevolmente in un successo'';
- ``scommetterei intorno al 2
 tentativo per la moneta, intorno
all'
tentativo per la moneta, intorno
all' 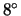 per l'ubriaco e intorno
al
per l'ubriaco e intorno
al 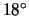 per il numero al lotto''.
per il numero al lotto''.
Ricaviamoci la funzione di probabilità e confrontiamola con le risposte
intuitive:
Questa distribuzione è chiamata geometrica in quanto
la funzione di probabilità è caratterizzata da tale progressione.
Verifichiamo, come esercizio,
che la funzione di probabilità soddisfa alla condizione di
normalizzazione. Infatti:
La funzione cumulativa 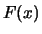 può essere ottenuta direttamente dalla
definizione:
può essere ottenuta direttamente dalla
definizione:
Essa vale 0 per 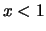 ,
mentre per i reali
,
mentre per i reali 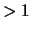 ha il valore che assume in corrispondenza
del numero intero
immediatamente inferiore. Si vede che, come deve essere,
per
ha il valore che assume in corrispondenza
del numero intero
immediatamente inferiore. Si vede che, come deve essere,
per
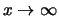 ,
, 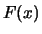 tende a 1.
La figura 6.6 mostra la distribuzione
geometrica per
tende a 1.
La figura 6.6 mostra la distribuzione
geometrica per 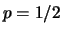 e
e 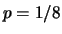 .
.
Figura:
Distribuzione geometrica per  uguale a 1/2 e a 1/8.
uguale a 1/2 e a 1/8.
 |
Per molti potrà essere una sorpresa scoprire che il massimo
di probabilità è in corrispondenza di  ,
indipendentemente da
,
indipendentemente da  .
Quindi la seconda domanda posta riguardo al problema dell'ubriaco
è in un certo senso controintuitiva.
Questo è dovuto ad una confusione fra ``il valore che ci aspettiamo''
e ``il valore più probabile''.
In effetti, anche se si accetta il fatto che la prova alla quale si
crede di più che si verifichi il successo sia la prima,
e che, per avere l'assoluta certezza, bisogna considerare un infinito
numero di prove,
permane ancora l'idea che il successo è atteso prima
nel caso di
lancio di una moneta che in quello di singolo estratto al lotto.
E in effetti questa
volta l'intuizione è corretta, a parte quantificare meglio
cosa si intende per previsione di un numero aleatorio.
.
Quindi la seconda domanda posta riguardo al problema dell'ubriaco
è in un certo senso controintuitiva.
Questo è dovuto ad una confusione fra ``il valore che ci aspettiamo''
e ``il valore più probabile''.
In effetti, anche se si accetta il fatto che la prova alla quale si
crede di più che si verifichi il successo sia la prima,
e che, per avere l'assoluta certezza, bisogna considerare un infinito
numero di prove,
permane ancora l'idea che il successo è atteso prima
nel caso di
lancio di una moneta che in quello di singolo estratto al lotto.
E in effetti questa
volta l'intuizione è corretta, a parte quantificare meglio
cosa si intende per previsione di un numero aleatorio.




Next: Sintesi di una distribuzione
Up: Variabili casuali e distribuzioni
Previous: Combinazione di molti processi
Indice
Giulio D'Agostini
2001-04-02
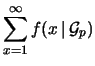
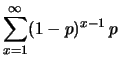
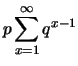
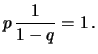
![]() ,
indipendentemente da
,
indipendentemente da ![]() .
Quindi la seconda domanda posta riguardo al problema dell'ubriaco
è in un certo senso controintuitiva.
Questo è dovuto ad una confusione fra ``il valore che ci aspettiamo''
e ``il valore più probabile''.
In effetti, anche se si accetta il fatto che la prova alla quale si
crede di più che si verifichi il successo sia la prima,
e che, per avere l'assoluta certezza, bisogna considerare un infinito
numero di prove,
permane ancora l'idea che il successo è atteso prima
nel caso di
lancio di una moneta che in quello di singolo estratto al lotto.
E in effetti questa
volta l'intuizione è corretta, a parte quantificare meglio
cosa si intende per previsione di un numero aleatorio.
.
Quindi la seconda domanda posta riguardo al problema dell'ubriaco
è in un certo senso controintuitiva.
Questo è dovuto ad una confusione fra ``il valore che ci aspettiamo''
e ``il valore più probabile''.
In effetti, anche se si accetta il fatto che la prova alla quale si
crede di più che si verifichi il successo sia la prima,
e che, per avere l'assoluta certezza, bisogna considerare un infinito
numero di prove,
permane ancora l'idea che il successo è atteso prima
nel caso di
lancio di una moneta che in quello di singolo estratto al lotto.
E in effetti questa
volta l'intuizione è corretta, a parte quantificare meglio
cosa si intende per previsione di un numero aleatorio.