



Next: Processo di Bernoulli
Up: Deviazione standard delle distribuzioni
Previous: Distribuzione uniforme fra 1
Indice
In questo caso i conti diventano più complessi. È preferibile
allora utilizzare le proprietà di valore atteso e varianza
sotto trasformazione lineare. Infatti,
se consideriamo la distribuzione
uniforme del paragrafo precedente, definita fra 1 ed  , si
vede come si possa ottenere la distribuzione uniforme fra
, si
vede come si possa ottenere la distribuzione uniforme fra  e
e 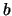 di valori distanziati di
di valori distanziati di
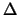 , mediante la trasformazione
Dalle
(6.29),
(6.41) e (6.40)
segue:
, mediante la trasformazione
Dalle
(6.29),
(6.41) e (6.40)
segue:
riottenendo sia il risultato precedente per la media
(vedi (6.30)) che,
come visto nel caso analogo,
una deviazione standard pari a circa al 30% dell'ampiezza
dell'intervallo appena  è sensibilmente maggiore di 1.
è sensibilmente maggiore di 1.




Next: Processo di Bernoulli
Up: Deviazione standard delle distribuzioni
Previous: Distribuzione uniforme fra 1
Indice
Giulio D'Agostini
2001-04-02
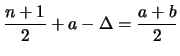
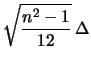
![$\displaystyle \frac{b-a}{\sqrt{12}}\,
\sqrt{\frac{n+1}{n-1}}\xrightarrow[n\gg 1]{}>\frac{b-a}{\sqrt{12}}\,,$](img1169.png)