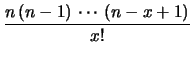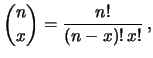Supponiamo di lanciare un dado e di essere interessati
all'uscita di un certo valore, per esempio il ``4''. Definiamo
successo ogni esito del lancio in cui si verifica il numero ``4''.
Pensiamo di dover eseguire
un certo numero ![]() di lanci ed esaminiamo la variabile
di lanci ed esaminiamo la variabile
![]() ``numero di successi'' (
``numero di successi'' (
![]() ). Vediamo quanto vale
la probabilità
della variabile casuale
). Vediamo quanto vale
la probabilità
della variabile casuale ![]() all'aumentare del numero dei lanci
(
all'aumentare del numero dei lanci
(![]() sta per successo e
sta per successo e ![]() sta per insuccesso):
sta per insuccesso):
da cui
![]() e
e
![]() . È immediato provare
che
. È immediato provare
che
![]() .
.
Notiamo l'analogia con lo sviluppo del binomio di Newton.
Infatti chiamando
![]() la probabilità di un successo nel singolo lancio (
la probabilità di un successo nel singolo lancio (
![]() nel nostro esempio) e
nel nostro esempio) e ![]() la probabilità di un insuccesso, le
la probabilità di un insuccesso, le
![]() corrispondono ai termini dello sviluppo di
corrispondono ai termini dello sviluppo di ![]() .
Questo è dovuto al fatto che
l'evento
.
Questo è dovuto al fatto che
l'evento ![]() successi e
successi e ![]() insuccessi si può presentare in
tanti modi diversi, ed esattamente
quante sono le possibilità di costituire, partendo da
insuccessi si può presentare in
tanti modi diversi, ed esattamente
quante sono le possibilità di costituire, partendo da ![]() elementi,
dei gruppetti
di
elementi,
dei gruppetti
di ![]() elementi ciacuno, indipendentemente dall'ordine con cui gli
elementi ciacuno, indipendentemente dall'ordine con cui gli
![]() elementi sono scelti. In termini matematici esse sono le
combinazioni di
elementi sono scelti. In termini matematici esse sono le
combinazioni di ![]() elementi
presi ``
elementi
presi ``![]() a
a ![]() ''.
La probabilità di ciascuno dei modi è pari
a
''.
La probabilità di ciascuno dei modi è pari
a
![]() .
Quindi, in generale, possiamo scrivere questa distribuzione di
probabilità, chiamata binomiale, come:
.
Quindi, in generale, possiamo scrivere questa distribuzione di
probabilità, chiamata binomiale, come:
Resta da calcolar quanto vale il coefficiente binomiale
Permutazioni: il numero totale dei
possibili modi
di disporre (``ordinare'',``mettere in fila'')
![]() oggetti si calcola considerando che
ci sono
oggetti si calcola considerando che
ci sono ![]() possibilità per
il primo,
possibilità per
il primo, ![]() per il secondo,
per il secondo, ![]() per il terzo e così via.
Cioè il numero di permutazioni di
per il terzo e così via.
Cioè il numero di permutazioni di ![]() oggetti è
pari a
oggetti è
pari a ![]() .
.
Combinazioni: supponiamo ora di dover scegliere un ![]() elementi da un insieme che ne contiene un numero
elementi da un insieme che ne contiene un numero ![]() senza curarsi dell'ordine con cui essi sono scelti. Ad esempio
in una classe di 25 persone si vogliono formare delle squadre di pallavolo
da 6 persone. Quante squadre diverse si possono fare? Abbiamo 25 modi per
scegliere la prima persona, 24 per la seconda e così via, cioè
senza curarsi dell'ordine con cui essi sono scelti. Ad esempio
in una classe di 25 persone si vogliono formare delle squadre di pallavolo
da 6 persone. Quante squadre diverse si possono fare? Abbiamo 25 modi per
scegliere la prima persona, 24 per la seconda e così via, cioè
![]() . Così facendo
abbiamo contato
. Così facendo
abbiamo contato ![]() volte ( ovvero il numero
di permutazioni di 6 elementi)
ogni squadra composta dagli stessi
giocatori ma estratti in modi diversi.
Quindi, in generale, bisogna divedere l'espressione precedentemente
trovata per
volte ( ovvero il numero
di permutazioni di 6 elementi)
ogni squadra composta dagli stessi
giocatori ma estratti in modi diversi.
Quindi, in generale, bisogna divedere l'espressione precedentemente
trovata per ![]() , ottenendo
, ottenendo