Next: Distribuzione binomiale - da
Up: Distribuzioni di probabilità di
Previous: Distribuzioni di probabilità di
Indice
Consideriamo ora la seconda schematizzazione di eventi legati
al processo di Bernoulli, descritta nel paragrafo 6.6.4.
Ovvero, interessandoci al numero di successi che possono
verificarsi in un certo numero di tentativi effettuati nelle
stesse condizioni.
Se analizziamo  prove indipendenti, per ciascuna
delle quali la probabilità
di successo è
prove indipendenti, per ciascuna
delle quali la probabilità
di successo è  ,
la variabile casuale
,
la variabile casuale  = ``numero totale di successi''
può andare da 0 a
= ``numero totale di successi''
può andare da 0 a  (da nessuno a tutti).
(da nessuno a tutti).
Ricaviamoci la funzione di probabilità, a partire dai
valori ``più facili''.
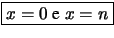
-
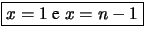
- Per
 si deve verificare un solo successo
e
si deve verificare un solo successo
e 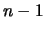 insuccessi. Quindi sembrerebbe, ad esempio, che
insuccessi. Quindi sembrerebbe, ad esempio, che
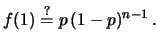 |
(7.1) |
Ma in realtà questa espressione dà la probabilità che
il successo si verifichi ad un certo tentativo (ad esempio al primo)
e gli insuccessi nei rimanenti
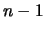 tentativi. Poiché abbiamo
tentativi. Poiché abbiamo  possibili tentativi
fra loro incompatibili
nei quali si può verificare il successo,
dobbiamo moltiplicare
l'espressione precedente per
possibili tentativi
fra loro incompatibili
nei quali si può verificare il successo,
dobbiamo moltiplicare
l'espressione precedente per  . Per
. Per 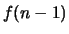 otteniamo un analogo risultato. Quindi:
otteniamo un analogo risultato. Quindi:
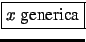
- Ne segue che l'espressione generale della funzione di probabilità
è data dalla probabilità che si verifichino
 successi
e
successi
e 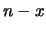 insuccessi, pari a
insuccessi, pari a
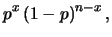 |
(7.2) |
moltiplicata per il numero di volte che, indipendentemente dall'ordine,
si possono ottenere gli  successi in
successi in  prove.
Questo numero è pari a quello delle
combinazioni semplici di
prove.
Questo numero è pari a quello delle
combinazioni semplici di  elementi presi
elementi presi  a
a  ,
che - ricordiamo - sono
date dai coefficienti binomiali,
indicati con
(vedi paragrafo 3.2.5).
La formula generale
della funzione di probabilità è quindi
,
che - ricordiamo - sono
date dai coefficienti binomiali,
indicati con
(vedi paragrafo 3.2.5).
La formula generale
della funzione di probabilità è quindi
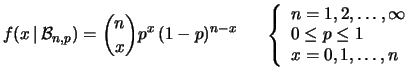 |
(7.3) |
Esplicitando l'espressione dei coefficienti binomiali,
la (7.3) può essere riscritta in modo
più pratico come
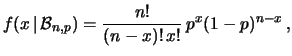 |
(7.4) |
ovvero
avendo indicato con 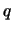 la probabilità di insuccesso
la probabilità di insuccesso 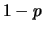 .
Per quanto riguarda la funzione di ripartizione
.
Per quanto riguarda la funzione di ripartizione 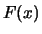 , in questo caso
essa non ha una espressione matematica semplice e va calcolata
dalla definizione stessa, sommando tutti i valori di
, in questo caso
essa non ha una espressione matematica semplice e va calcolata
dalla definizione stessa, sommando tutti i valori di 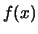 fino
al numero intero positivo immediatamente precedente ad
fino
al numero intero positivo immediatamente precedente ad  (ricordiamo
ancora una volta
che
(ricordiamo
ancora una volta
che 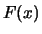 è convenzionalmente definita su tutto l'asse reale).
è convenzionalmente definita su tutto l'asse reale).




Next: Distribuzione binomiale - da
Up: Distribuzioni di probabilità di
Previous: Distribuzioni di probabilità di
Indice
Giulio D'Agostini
2001-04-02
![]() prove indipendenti, per ciascuna
delle quali la probabilità
di successo è
prove indipendenti, per ciascuna
delle quali la probabilità
di successo è ![]() ,
la variabile casuale
,
la variabile casuale ![]() = ``numero totale di successi''
può andare da 0 a
= ``numero totale di successi''
può andare da 0 a ![]() (da nessuno a tutti).
(da nessuno a tutti).