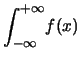
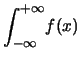
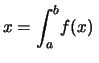 d
d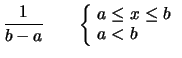 |
(8.4) |
Essendo la funzione densità di probabilità costante,
la funzione di ripartizione è lineare nell'intervallo ![]() ,
come si verifica
facilmente:
,
come si verifica
facilmente:
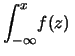 |
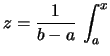 d d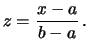 d d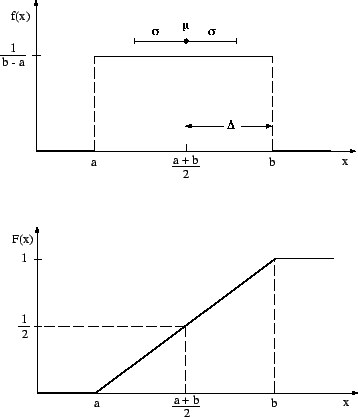 |
La figura 8.2 mostra la funzione di densità di probabilità e la funzione di ripartizione della distribuzione uniforme.
Calcoliamo il valore valore atteso e la varianza di ![]() (previo il calcolo di
E
(previo il calcolo di
E![]() ):
):
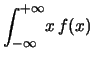 E E |
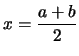 d d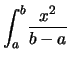 |
||
| E |
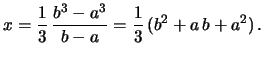 d d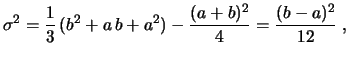 |
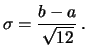
| (8.5) |
La distribuzione uniforme continua può essere pensata come il limite della distribuzione discreta (vedi paragrafo 6.6.2) quando il numero di punti tende a infinito e la spaziatura a zero. Si riottengono infatti gli stessi valori di media e deviazione standard.
La distribuzione uniforme viene impiegata
nella trattazione degli
errori di misura ogni qual volta si sa con sicurezza che una
certa variabile è contenuta in un certo intervallo, ma non si
ha alcun motivo per ritenere alcuni valori più plausibili di altri.
Per queste applicazioni è conveniente chiamare la larghezza
dell'intervallo
![]() , in quanto spesso
si usa dire che la variabile può verificarsi uniformemente
nell'intervallo
, in quanto spesso
si usa dire che la variabile può verificarsi uniformemente
nell'intervallo
![]() , dove
, dove 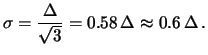 sta per il centro dell'intervallo.
Ne segue che
sta per il centro dell'intervallo.
Ne segue che
| (8.6) |
Un altro uso della uniforme continua è nelle simulazioni al calcolatore. Infatti, mediante opportune tecniche è possibile, a partire da una variabile distribuita uniformemente, costruire altre variabili distribuite a piacere. Il prossimo paragrafo è da considerare come una breve e interessante parentesi su tale argomento.