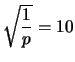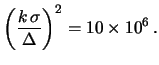Next: Teorema di Bernoulli
Up: Legge dei grandi numeri
Previous: Legge dei grandi numeri
Indice
Prendiamo  variabili casuali
variabili casuali 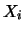 i cui valori sono descritti da una distribuzione di probabilità
che sia la stessa per tutte le variabili. Si può pensare quindi
ad un esperimento condotto
i cui valori sono descritti da una distribuzione di probabilità
che sia la stessa per tutte le variabili. Si può pensare quindi
ad un esperimento condotto  volte sotto le stesse condizioni.
Tale distribuzione ha valore atteso
volte sotto le stesse condizioni.
Tale distribuzione ha valore atteso 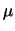 e deviazione standard
e deviazione standard
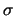 .
.
Interessiamoci alla media aritmetica
effettuata sui valori di 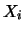 che si verificheranno.
Come abbiamo già visto,
anche
che si verificheranno.
Come abbiamo già visto,
anche
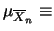 è una variabile casuale,
in quanto funzione di variabili casuali.
Abbiamo già visto che
è una variabile casuale,
in quanto funzione di variabili casuali.
Abbiamo già visto che
Per quanto detto nel paragrafo 7.10
ci aspettiamo che al crescere di  diminuisce
la probabilità di trovare valori di
diminuisce
la probabilità di trovare valori di
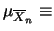 ``molto distanti'' da
``molto distanti'' da 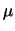 . Ripetiamo il ragionamento, facendo uso
della disuguaglianza di Cebicev, applicata alla variabile
casuale
. Ripetiamo il ragionamento, facendo uso
della disuguaglianza di Cebicev, applicata alla variabile
casuale
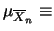 (in realtà si può fare anche uso della
forma esatta della distribuzione di probabilità di
(in realtà si può fare anche uso della
forma esatta della distribuzione di probabilità di
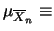 ,
che vedremo fra breve parlando del teorema del limite centrale):
Inserendo i valori di
,
che vedremo fra breve parlando del teorema del limite centrale):
Inserendo i valori di
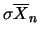 e
e
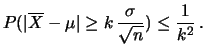 si ottiene
si ottiene
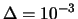 |
(10.50) |
L'interpretazioone di questa disuguaglianza è che,
data una certa 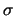 , fissato un certo livello di probabilità
, fissato un certo livello di probabilità
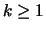 e un valore dello scarto
e un valore dello scarto 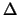 piccoli a piacere, è sufficiente
effettuare un numero di prove corrispondentemente grande
affinche' la probabiltà di osservare uno scarto assoluto
maggiore di
piccoli a piacere, è sufficiente
effettuare un numero di prove corrispondentemente grande
affinche' la probabiltà di osservare uno scarto assoluto
maggiore di 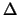 sia inferiore al valore di probabilità prescelto.
sia inferiore al valore di probabilità prescelto.
Facciamo un esempio numerico: prendiamo 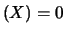 , il valore di probabilità
dell'1% e uno scarto
, il valore di probabilità
dell'1% e uno scarto
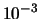 .
Riformuliamo il problema: quante prove devo fare
per essere sicuro al 99% che
.
Riformuliamo il problema: quante prove devo fare
per essere sicuro al 99% che
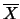 non differirà per più di
non differirà per più di
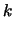 da
da 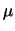 ? Dalla 10.50 abbiamo
che
? Dalla 10.50 abbiamo
che
Se scegliamo
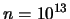 abbiamo bisogno di
abbiamo bisogno di
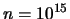 per avere lo stesso livello di sicurezza.
Mantenendo
per avere lo stesso livello di sicurezza.
Mantenendo
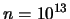 , possiamo richiedere un livello di
sicurezza del 99.99% che lo scarto sia contenuto entro
, possiamo richiedere un livello di
sicurezza del 99.99% che lo scarto sia contenuto entro 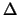 ,
ma allora avremo bisogno di
,
ma allora avremo bisogno di
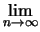 prove. E così via.
Quindi, quando il numero di prove è grandissimo
siamo ``praticamente'' sicuri di trovare
prove. E così via.
Quindi, quando il numero di prove è grandissimo
siamo ``praticamente'' sicuri di trovare
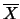 prossimo a
prossimo a 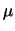 .
Possiamo esprimere il risultato dicendo che
.
Possiamo esprimere il risultato dicendo che
``
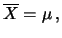
''
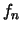
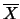 entro
entro 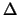 da
da 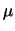 (anche se
(anche se 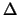 è
relativamente grande, purché non superiore all'intervallo
di definizione di
è
relativamente grande, purché non superiore all'intervallo
di definizione di 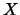 ).
).




Next: Teorema di Bernoulli
Up: Legge dei grandi numeri
Previous: Legge dei grandi numeri
Indice
Giulio D'Agostini
2001-04-02
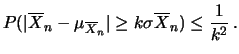
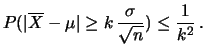 si ottiene
si ottiene
![]() , il valore di probabilità
dell'1% e uno scarto
, il valore di probabilità
dell'1% e uno scarto
![]() .
Riformuliamo il problema: quante prove devo fare
per essere sicuro al 99% che
.
Riformuliamo il problema: quante prove devo fare
per essere sicuro al 99% che
![]() non differirà per più di
non differirà per più di
![]() da
da ![]() ? Dalla 10.50 abbiamo
che
? Dalla 10.50 abbiamo
che