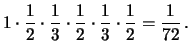Next: Legge delle alternative
Up: Altre proprietà della probabilità
Previous: Altre proprietà della probabilità
Indice
Le relazioni (4.16) e (4.21)
possono essere estese al caso di  eventi, ottenendo
la legge della moltiplicazione delle probabilità,
dall'espressione più generale
eventi, ottenendo
la legge della moltiplicazione delle probabilità,
dall'espressione più generale
In analogia al semplice caso di due eventi, quando si verifica che
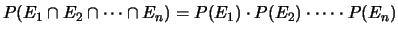 |
(4.23) |
gli  eventi fra di loro indipendenti.
Si noti come l'indipendenza fra ciascuna delle coppie di eventi
eventi fra di loro indipendenti.
Si noti come l'indipendenza fra ciascuna delle coppie di eventi
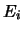 e
e 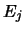 non implica la 4.23.
non implica la 4.23.
Figura:
Esempio di probabilità condizionata.
 |
Come esempio di applicazione della (4.22)
consideriamo il labirinto della figura 4.4.
La probabilità di arrivare al tesoro (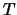 ) passando prima
per il bivio 5 vale (associamo alla biforcazione numero
) passando prima
per il bivio 5 vale (associamo alla biforcazione numero 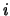 l'evento
l'evento 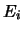 ).
).




Next: Legge delle alternative
Up: Altre proprietà della probabilità
Previous: Altre proprietà della probabilità
Indice
Giulio D'Agostini
2001-04-02
![]() ) passando prima
per il bivio 5 vale (associamo alla biforcazione numero
) passando prima
per il bivio 5 vale (associamo alla biforcazione numero ![]() l'evento
l'evento ![]() ).
).