Subjective or objective Bayesian theory?

Once you have understood that probability and frequencies are different concepts, that probability of hypothesis is a useful and natural concept for reporting results, that Bayes' theorem is a powerful tool for updating probability and learning from data, that priors are important and pretending that they do not exist is equivalent to assuming them flat, and so on, it is difficult to then take a step back. However, it is true that there is no single shared point of view among those who, generally speaking, support the Bayesian approach. I don't pretend that I can provide an exhaustive analyse of the situation here, or to be unbiased about this matter either.

The main schools of thought are the `subjectivists' and the `objectivists'. The dispute may look strange to an outsider, if one thinks that both schools use probability to represent degrees of belief. Nevertheless, objectivists want to minimize the person's contribution to the inference, by introducing reference priors (for example Jeffreys' priors[29]) or other constraints, such as maximum entropy (for an overview see Refs. [19] and [78]). The motto is ``let the data speak for themselves''. I find this subject highly confusing, and even Bernardo and Smith (Bernardo is one of the key persons behind reference priors) give the impression of contradicting themselves often on this point as, for example, when the subject of reference analysis is introduced:

``to many attracted to the formalism of the Bayesian inferential paradigm, the idea of a non-informative prior distribution, representing `ignorance' and `letting the data speak for themselves' has proved extremely seductive, often being regarded as synonymous with providing objective inferences. It will be clear from the general subjective perspective we have maintained throughout this volume, that we regard this search for `objectivity' to be misguided. However, it will also be clear from our detailed development in Section 5.4 that we recognize the rather special nature and role of the concept of a `minimal informative' prior specification - appropriately defined! In any case, the considerable body of conceptual and theoretical literature devoted to identifying `appropriate' procedures for formulating prior representations of `ignorance' constitutes a fascinating chapter in the history of Bayesian Statistics. In this section we shall provide an overview of some of the main directions followed in this search for a Bayesian `Holy Grail'.[19]

In my point of view, the extreme idea along this line is represented by the Jaynes' `robot' (``In order to direct attention to constructive things and away from controversial irrelevance, we shall invent an imaginary being. Its brain is to be designed by us, so that it reasons according to certain defined rules. These rules will be deduced from simple desiderata which, it appears to us, would be desirable in human brains''[79]).

As far as I understand it, I see only problems with objectivism, although I do agree on the notion of a commonly perceived objectivity, in the sense of intersubjectivity (see Section ). Frankly, I find probabilistic evaluations made by a coherent subjectivist, assessed under personal responsibility, to be more trustworthy and more objective than values obtained in a mechanical way using objective prescriptions[22].

Moving to a philosophical level deeper than this kind of angels' sex debate (see Section ), there is the important issue of what an event is. All events listed in Section (apart from that of point 4) are somehow verifiable. Perhaps one will have to wait until tomorrow, the end of 1999, or 2010, but at a certain point the event may become certain, either true or false. However, one can think about other events, examples of which have been shown in these notes, that are not verifiable, either for a question of principle, or by accident.

• The old friend could die, carrying with him the secret of whether he had been cheating, or simply lucky (Section ).
• The particle interacts with the detector (Section ) and continues its flight: was it really a $\pi$ or a $\mu$?
• Using our best knowledge about temperature measurement we can state that the temperature of a room at a certain instant is $21.7\pm 0.3\,^\circ$C with 95% probability (Section ); after the measurement the window is opened, the weather changes, the thermometer is lost: how is it possible to verify the event ` $21.4\le T/^\circ$C$\le 22.0$'?

This problem is present every time we make a probabilistic statement about physics quantities. It is present not only when a measurand is critically time dependent (the position of a plane above the Atlantic), but also in the case of fundamental constants. In this latter case we usually believe in the progress of science and thus we hope that the quantity will be measured so well in the future that it will one day become a kind of exact value, in comparison to today's uncertainty. But it is absurd to think that one day we will be able to `open an electron' and read on a label all its properties with an infinite number of digits. This means that for scientific applications it is convenient to enlarge the concept of an event (see Section ), releasing the condition of verifiability.^8.20At this point the normative role of the hypothetical coherent bet becomes crucial. A probability evaluation, made by an honest person well-trained in applying coherence on verifiable events, becomes, in my opinion, the only means by which degrees of belief can be exchanged among rational people. We have certainly reached a point in which the domain of physics, metaphysics and moral overlap, but it looks to me that this is exactly the way in which science advances.

It seems to me that almost all Bayesian schools support this idea of the extended meaning of an event, explicitly or tacitly (anyone who speaks about $f(\theta)$, with $\theta$ a parameter of a distribution, does it). A more radical point of view, which is very appealing from the philosophical perspective, but more difficult to apply (at least in physics), is the predictive approach (or operational subjectivism), along the lines of de Finetti's thinking. The concept of probability is strictly applied only to real observables, very precisely (`operationally') defined. The events are all associated with discrete uncertain numbers (integer or rational), in the simplest case 1 or 0 if there are only two possibilities (true or false). 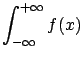Having excluded non-observables, it makes no sense to speak of $f(\mu\,\vert\,$data$)$, but only of $f(x\,\vert\,$data$)$, where $X$ stands for a future (or, in general, not yet known) observation. For the moment I prefer to stick to our `metaphysical' true values, but I encourage anyone who is interested in this subject to read Lad's recent book[80], which also contains a very interesting philosophical and historical introduction to the subject.