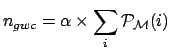Conclusion and discussion

This paper is mainly on methodological issues related to model comparisons in critical, frontier physics cases where the prior knowledge is relevant.

We have given reasons of why `conventional statistics' (i.e. the collection of frequentistic prescriptions) does not adequately approach the problem of model comparison, mainly because of impossibility of classify hypotheses in a probability scale and of the pretension that good criteria to state what is `significant' can be derived from the properties of the null hypothesis alone, without considering the details of the alternative hypotheses.²

Within the so called Bayesian framework, we have started from the basic observation that the most a probability theory should do is to provide rules to modify our beliefs on the light of experimental data. Beliefs can be about the values of the parameters of a model or about alternative models. As far as beliefs on model parameters are concerned, we have shown that the likelihood, rescaled to its insensitivity limit value (the ${\cal R}$ function, or `relative belief updating factor'), represents a good, prior independent way of summarizing the information contained in the data with respect to a given model. Indeed, when this method is applied to the Explorer-Nautilus data, from the visual inspection of the ${\cal R}$ function the reader gets, for each model, an immediate overview of what the data say about the number of events involved in the observation. The $\alpha$ values for which the relative belief updating factor is maximum correspond to a total number of g.w. events in the data (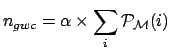$n_{gwc}$) about 10 for all three Galactic models. For those who share beliefs that numbers of this order of magnitude or more are possible (and that one of the three models is the correct one), the ${\cal R}$ can be translated into a result $n_{gwc}\approx 10\pm 5$ (or a rate on Earth of $\approx 1.0\pm 0.5$).

Going to the model comparison, we have shown the unavoidable complication due to the fact that each model depends on a free parameter ($\alpha$) and, hence, the Bayes factors depend on the prior pdf of this parameter, i.e. $f_{\circ_{\cal M}}(\alpha)$. Since the models used do not come with a kind of reference $f_{\circ_{\cal M}}(\alpha)$ (we hope that more work will be done in this direction) we had to do some choices and we have given the results under different scenarios, from the most negative one (``there is no chance that the models produce something observable, given the present energy sensitivity'') to some others in which $\alpha$ above 1 are conceivable (described by the priors we have called in the text `moderate' and 'uniform'). Given these scenarios the Galactic Center model gets preferred over the others by a Bayes factor of about 2:1.

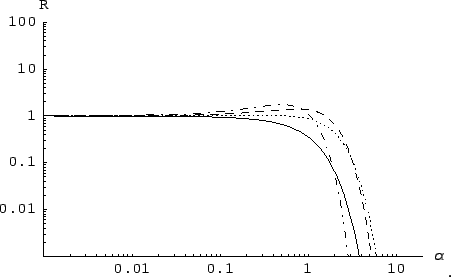
We would like to end replying to the objection, arisen often in discussions, that ``the plot with coincidences grouped in bins of sidereal time provides the same information of that in which coincidences are grouped in bins of solar time''. This might be true if one is blindly looking for ``statistical significance'', following strictly frequentistic prescriptions, which, as explained above, we do not consider the proper way to go.

To answer this objection we have done the exercise of applying exactly the same analysis with the same models to the data grouped in bins of solar time.

Figure 4: Same as Fig. 3, but for data grouped in solar time bins

Table 3: Same as Tab. 2, but for data grouped in solar time bins

	`sceptical'	`moderate'	`uniform'
$$\begin{array}{lr} & f_0(\alpha) \\ & \\ \mbox{Model} & \end{array}$$
	1.0	0.5	0.1
	1.1	1.2	0.3
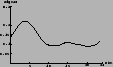	1.0	0.9	0.2
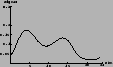	1.2	1.2	0.2

The results are given in Fig. 4 and Tab. 3, which have the analogous meaning of Fig. 3 and Tab. 2. The ${\cal R}$ functions do not show values of $\alpha$ particularly preferred by the data: they have approximately a smoothed step-function shape which divides the orders of magnitudes of $\alpha$ (on the right side) that are excluded from those in which the experiment loses sensitivity. 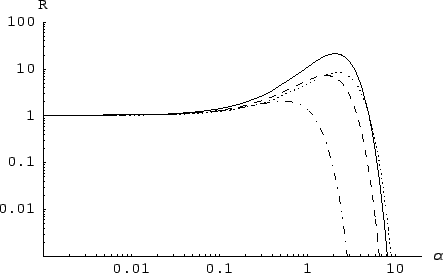This is more ore less what we could get distributing 34 entries in 48 bins according to a multinomial distribution: small differences in the shape of ${\cal R}_{\cal M}(\alpha)$ depend on the individual occurrence of the multinomial data set (but never forget that the multinomial distribution does not forbid strong clustering of the entries around one bin!).

The lesson from this exercise is that the Explorer-Nautilus 2001 data, plotted as a function of a sensible physical quantity and compared with physically motivated models, does not provide the same information of any random sample. Indeed, the evidence in support of the models is not enough to modify strongly our beliefs, but it is certainly at the level of ``stay tuned'', waiting for results of the 2003 run.