


Next: Predictive distributions
Up: Inferring numerical values of
Previous: Inference from a data
Multidimensional case -- Inferring 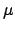 and
and 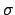 of a Gaussian
of a Gaussian
So far we have only inferred one parameter of a model.
The extension to many parameters
is straightforward. Calling
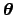 the set of parameters
and
the set of parameters
and
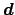 the data, Bayes' theorem becomes
the data, Bayes' theorem becomes
Equation (52) gives the posterior for the full
parameter vector
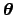 .
Marginalization (see Tab. 1)
allows one to
calculate the probability distribution for a single parameter,
for example,
.
Marginalization (see Tab. 1)
allows one to
calculate the probability distribution for a single parameter,
for example,
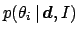 ,
by integrating over the remaining
parameters. The marginal distribution
,
by integrating over the remaining
parameters. The marginal distribution
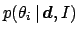 is then the complete result of the Bayesian
inference on the parameter
is then the complete result of the Bayesian
inference on the parameter 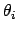 . Though the characterization
of the marginal is done in the usual way described in
Sect. 5.1, there is often the interest to
summarize some characters of the multi-dimensional
posterior that are unavoidably lost in the marginalization
(imagine marginalization as a kind of geometrical projection).
Useful quantities are the covariances between parameters
. Though the characterization
of the marginal is done in the usual way described in
Sect. 5.1, there is often the interest to
summarize some characters of the multi-dimensional
posterior that are unavoidably lost in the marginalization
(imagine marginalization as a kind of geometrical projection).
Useful quantities are the covariances between parameters
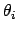 and
and 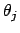 , defined as
, defined as
As is well know, quantities which give a more intuitive idea
of what is going on are the correlation coefficients, defined
as
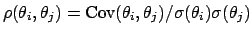 .
Variances and covariances form the
covariance matrix
.
Variances and covariances form the
covariance matrix
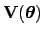 , with
, with
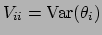 and
and
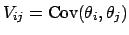 .
We recall also that convenient formulae to calculate variances and covariances
are obtained from the expectation of the products
.
We recall also that convenient formulae to calculate variances and covariances
are obtained from the expectation of the products
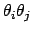 ,
together with the expectations of the parameters:
,
together with the expectations of the parameters:
As a first example of a multidimensional distribution from a
data set, we can think, again, at the inference of the parameter
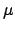 of a Gaussian distribution, but in the case that also
of a Gaussian distribution, but in the case that also
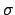 is unknown and needs to be determined by the data.
From Eqs. (52), (50) and
(25), with
is unknown and needs to be determined by the data.
From Eqs. (52), (50) and
(25), with 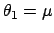 and
and
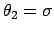 and neglecting overall normalization, we obtain
and neglecting overall normalization, we obtain
The closed form of Eqs. (56) and 57)
depends on the prior and, perhaps, for
the most realistic choice of
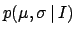 , such a
compact solution does not exists. But this is not an essential issue,
given the present computational power.
(For example, the shape of
, such a
compact solution does not exists. But this is not an essential issue,
given the present computational power.
(For example, the shape of
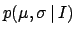 can be easily inspected
by a modern graphical tool.)
We want to stress here
the conceptual simplicity of the Bayesian solution to the problem.
[In the case the data set contains some more than a dozen of
observations, a flat
can be easily inspected
by a modern graphical tool.)
We want to stress here
the conceptual simplicity of the Bayesian solution to the problem.
[In the case the data set contains some more than a dozen of
observations, a flat
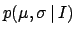 , with the constraint
, with the constraint
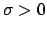 , can be considered a good practical choice.]
, can be considered a good practical choice.]



Next: Predictive distributions
Up: Inferring numerical values of
Previous: Inference from a data
Giulio D'Agostini
2003-05-13
![]() the set of parameters
and
the set of parameters
and
![]() the data, Bayes' theorem becomes
the data, Bayes' theorem becomes