


Next: Hierarchical modelling and hyperparameters
Up: Inferring numerical values of
Previous: Multidimensional case
Predictive distributions
A related problem is to `infer' what an experiment will observe
given our best knowledge of the underlying theory and its parameters.
Infer is within quote marks because the term is usually used for
model and parameters, rather than for observations. In this
case people prefer to speak about prediction (or prevision).
But we recall that in the Bayesian reasoning there is conceptual
symmetry between the uncertain quantities which enter the
problem. Probability density functions describing not yet observed
event are referred to as predictive distributions.
There is a conceptual difference with the likelihood, which
also gives a probability of observation, but under different hypotheses,
as the following example clarifies.
Given 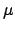 and
and 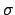 , and assuming a Gaussian model,
our uncertainty about a `future'
, and assuming a Gaussian model,
our uncertainty about a `future' 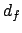 is described by the Gaussian
pdf Eq. (25) with
is described by the Gaussian
pdf Eq. (25) with 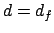 . But this holds only
under that particular hypothesis for
. But this holds only
under that particular hypothesis for 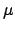 and
and 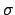 ,
while, in general, we are also uncertain about these values too.
Applying the decomposition formula (Tab. 1) we get:
,
while, in general, we are also uncertain about these values too.
Applying the decomposition formula (Tab. 1) we get:
Again, the integral might be technically difficult, but the solution
is conceptually simple. Note that, though the decomposition formula
is a general result of probability theory, it can be applied to
this problem only in the subjective approach.
An analytically easy, insightful case is that of experiments with
well-known 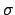 's. Given a past observation
's. Given a past observation 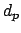 and a vague prior,
and a vague prior,
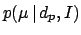 is Gaussian around
is Gaussian around 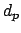 with variance
with variance 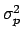 [note that, with respect to
[note that, with respect to
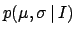 of Eq.(58),
it has been made explicit that
of Eq.(58),
it has been made explicit that 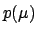 depend on
depend on 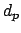 ].
].
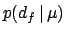 is Gaussian around
is Gaussian around 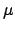 with variance
with variance 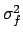 . We get finally
. We get finally



Next: Hierarchical modelling and hyperparameters
Up: Inferring numerical values of
Previous: Multidimensional case
Giulio D'Agostini
2003-05-13
![]() and
and ![]() , and assuming a Gaussian model,
our uncertainty about a `future'
, and assuming a Gaussian model,
our uncertainty about a `future' ![]() is described by the Gaussian
pdf Eq. (25) with
is described by the Gaussian
pdf Eq. (25) with ![]() . But this holds only
under that particular hypothesis for
. But this holds only
under that particular hypothesis for ![]() and
and ![]() ,
while, in general, we are also uncertain about these values too.
Applying the decomposition formula (Tab. 1) we get:
,
while, in general, we are also uncertain about these values too.
Applying the decomposition formula (Tab. 1) we get:
![]() 's. Given a past observation
's. Given a past observation ![]() and a vague prior,
and a vague prior,
![]() is Gaussian around
is Gaussian around ![]() with variance
with variance ![]() [note that, with respect to
[note that, with respect to
![]() of Eq.(58),
it has been made explicit that
of Eq.(58),
it has been made explicit that ![]() depend on
depend on ![]() ].
].
![]() is Gaussian around
is Gaussian around ![]() with variance
with variance ![]() . We get finally
. We get finally
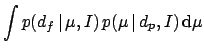
![$\displaystyle \frac{1}{\sqrt{2\pi}\,\sqrt{\sigma_p^2+\sigma_f^2}}
\,\exp \left[-\frac{(d_f-d_p)^2}{2\,(\sigma_p^2+\sigma_f^2)}\right] \,.$](img265.png)