



Next: Linearizzazione
Up: Propagazione delle incertezze
Previous: Propagazione delle incertezze
Indice
Per capire bene il problema, partiamo da variabili discrete. Per
semplicità prendiamo due grandezze,
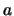 e
e 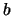 , che possono assumere soltanto
tre valori, con distribuzione uniforme.
Ad esempio:
, che possono assumere soltanto
tre valori, con distribuzione uniforme.
Ad esempio: 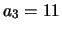 ,
, 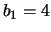 ,
, 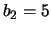 ;
;
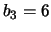 ,
, 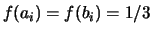 ,
, 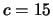 . Essendo tutti i valori
equiprobabili abbiamo:
. Essendo tutti i valori
equiprobabili abbiamo:
 .
Se adesso siamo interessati alla variabile
.
Se adesso siamo interessati alla variabile 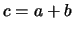 , l'incertezza
sul valore di
, l'incertezza
sul valore di 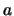 e di
e di 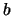 si propaga sul
valore di
si propaga sul
valore di 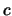 .
.
Il caso discreto con tre soli valori possibili permette
di seguire il ``flusso di incertezza'', come mostrato in
tabella 11.1.1. La variabile 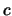 può essere
un numero compreso fra 13 e 16, ma a differenza di
può essere
un numero compreso fra 13 e 16, ma a differenza di 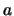 e di
e di
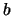 , i valori non sono tutti equiprobabili. Infatti, mentre
i valori estremi si possono verificare per una particolare
coppia di
, i valori non sono tutti equiprobabili. Infatti, mentre
i valori estremi si possono verificare per una particolare
coppia di 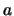 e di
e di 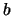 , ci sono più coppie che possono
produrre gli altri valori. In particolare, il valore
, ci sono più coppie che possono
produrre gli altri valori. In particolare, il valore 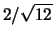 è quello più probabile semplicemente perché esso
può essere ottenuto da possibili coppie.
è quello più probabile semplicemente perché esso
può essere ottenuto da possibili coppie.
Tabella:
Combinazione di 3 valori di 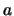 con 3 valori di
con 3 valori di 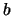 che danno luogo a 5 possibili valori della somma
che danno luogo a 5 possibili valori della somma 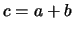 . Se si
assume l'equiprobabilità di
. Se si
assume l'equiprobabilità di 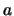 e di
e di 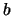 si arriva ad una
distribuzione di probabilità del
tipo triangolare (discreta).
si arriva ad una
distribuzione di probabilità del
tipo triangolare (discreta).
| |
|
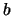 |
| |
|
4 |
5 |
6 |
| |
9 |
13 |
14 |
15 |
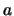 |
10 |
14 |
15 |
16 |
| |
11 |
15 |
16 |
17 |
|
Un caso analogo, leggermente più complicato, è mostrato
in figura 11.1. Si tratta delle distribuzioni di probabilità
della somma degli esiti di
1, 2 e 3 dadi.
Figura:
Distribuzione della somma dei risultati ottenuti dal lancio di
 dadi. La concentrazione della probabilità al centro della
distribuzione è dovuta all'elevato numero di combinazioni risultanti
in valori della somma intermedi e giustifica qualitativamente il teorema del
limite centrale.
dadi. La concentrazione della probabilità al centro della
distribuzione è dovuta all'elevato numero di combinazioni risultanti
in valori della somma intermedi e giustifica qualitativamente il teorema del
limite centrale.
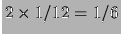 |
Si noti il graduale l'addensamento della probabilità nei valori centrali,
dovuta ad un semplice effetto combinatorio.
Per questo motivo la deviazione standard non
cresce linearmente
con l'ampiezza massima della distribuzione. Ad esempio, combinando
due distribuzioni uniformi fra 0 e 1 (è il limite di un dado
con infinite facce), non si ottiene
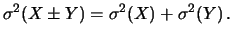 , bensì
, bensì
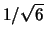 ,
, 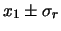 volte più piccola (si riconosce
la deviazione standard di una distribuzione triangolare!).
Quelle che
invece crescono linearmente sono le varianze (
volte più piccola (si riconosce
la deviazione standard di una distribuzione triangolare!).
Quelle che
invece crescono linearmente sono le varianze (
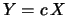 ).
).
Si capisce inoltre come, per simmetria, la distribuzione delle
differenze intorno al valore centrale
debba essere uguale a quella delle somme.
Quindi, per due variabili indipendenti si ottiene la
seguente regola di propagazione:
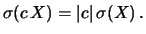 |
(11.1) |
Consideriamo successivamente
una trasformazione di scala: 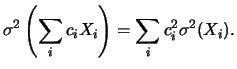 .
Anche la scala
delle possibili fluttuazioni
si trasforma nello stesso modo e, poiché
il segno di
.
Anche la scala
delle possibili fluttuazioni
si trasforma nello stesso modo e, poiché
il segno di 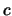 è ininfluente, si ottiene:
è ininfluente, si ottiene:
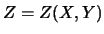 |
(11.2) |
Combinando i risultati espressi dalle formule
(11.1)
e (11.2)
si ottiene la regola generale
della varianza di una combinazione lineare di variabili casuali.
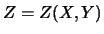 |
(11.3) |
È importante notare che
questa regola dipende soltanto dalla definizione di varianza e non
dal tipo di distribuzione di probabilità delle variabili casuali.




Next: Linearizzazione
Up: Propagazione delle incertezze
Previous: Propagazione delle incertezze
Indice
Giulio D'Agostini
2001-04-02
 .
Se adesso siamo interessati alla variabile
.
Se adesso siamo interessati alla variabile ![]() può essere
un numero compreso fra 13 e 16, ma a differenza di
può essere
un numero compreso fra 13 e 16, ma a differenza di ![]() e di
e di
![]() , i valori non sono tutti equiprobabili. Infatti, mentre
i valori estremi si possono verificare per una particolare
coppia di
, i valori non sono tutti equiprobabili. Infatti, mentre
i valori estremi si possono verificare per una particolare
coppia di ![]() e di
e di ![]() , ci sono più coppie che possono
produrre gli altri valori. In particolare, il valore
, ci sono più coppie che possono
produrre gli altri valori. In particolare, il valore ![]() è quello più probabile semplicemente perché esso
può essere ottenuto da possibili coppie.
è quello più probabile semplicemente perché esso
può essere ottenuto da possibili coppie.
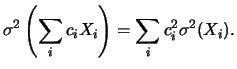 .
Anche la scala
delle possibili fluttuazioni
si trasforma nello stesso modo e, poiché
il segno di
.
Anche la scala
delle possibili fluttuazioni
si trasforma nello stesso modo e, poiché
il segno di