



Next: Come tener conto degli
Up: Propagazione delle incertezze
Previous: Linearizzazione
Indice
Incertezze relative
Riprendiamo la (11.4) estesa al caso generale,
ovvero nel caso di
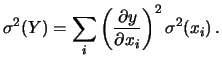
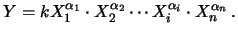
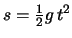 |
(11.7) |
Un caso particolarmente interessante si presenta quando
la dipendenza di  da
da 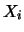 è data da una funzione monomia, ovvero
Molte leggi fisiche sono infatti di questo tipo (
è data da una funzione monomia, ovvero
Molte leggi fisiche sono infatti di questo tipo (
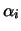 ,
,
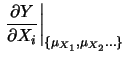 , etc). La derivata di
, etc). La derivata di 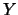 rispetto alla generica
rispetto alla generica 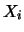 si ottiene diminuendo di 1 il grado della potenza
di
si ottiene diminuendo di 1 il grado della potenza
di 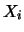 e moltiplicando per
e moltiplicando per 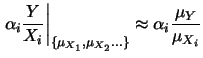 . Questo è equivalente
a moltiplicare la
. Questo è equivalente
a moltiplicare la 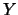 stessa per
stessa per 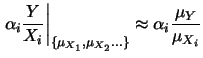 e poi dividere tutto per
e poi dividere tutto per
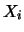 . Si ha quindi:
. Si ha quindi:
dove dalla formula (11.8) abbiamo sostituito,
come sopra, ``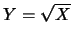 '' con
'' con 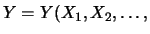 e abbiamo introdotto
e abbiamo introdotto
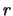 ad indicare l'incertezza relativa. Quindi, nel caso di funzioni
monomie il contributo all'incertezza relativa
dato da ciascuna variabile di ingresso è pari
alla sua incertezza relativa moltiplicata per il modulo della potenza.
I vari contributi si combinano poi quadraticamente. Si noti come
l'incertezza relativa su
ad indicare l'incertezza relativa. Quindi, nel caso di funzioni
monomie il contributo all'incertezza relativa
dato da ciascuna variabile di ingresso è pari
alla sua incertezza relativa moltiplicata per il modulo della potenza.
I vari contributi si combinano poi quadraticamente. Si noti come
l'incertezza relativa su 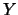 può essere anche inferiore
a quella su
può essere anche inferiore
a quella su 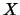 se
se
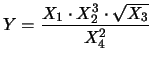 (ad esempio
(ad esempio
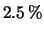 ).
Si noti inoltre come la 11.10 è valida anche
per le incertezze relative espresse in valori percentuali.
).
Si noti inoltre come la 11.10 è valida anche
per le incertezze relative espresse in valori percentuali.
Il vantaggio pratico di utilizzare, ogni volta che è possibile,
la propagazione delle incertezze relative è legato
al fatto che, siccome
quello che veramente importa ai fini della qualità della misura
è l'incertezza relativa, essa permette di capire quali sono
le grandezze più critiche, sulle eventualmente quali intervenire.
Questo è particolarmente vero se si usa la formula
11.10 scrivendo esplicitamente tutti gli ``addendi'',
invece di fare automaticamente. Ad esempio se si ha
con incertezze relative delle grandezze di ingresso, espresse in %,
pari a 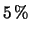 ,
, 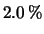 ,
, 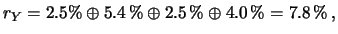 e
e 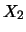 , è opportuno scrivere
(***controllare***)
da cui si capisce subito che per migliorare il risultato bisogna
misurare meglio
, è opportuno scrivere
(***controllare***)
da cui si capisce subito che per migliorare il risultato bisogna
misurare meglio 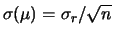 , anche se era già la grandezza
conosciuta più precisamente. A poco serve, invece,
misurare meglio
, anche se era già la grandezza
conosciuta più precisamente. A poco serve, invece,
misurare meglio 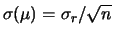 , sebbene sia nota soltanto al 5%.
, sebbene sia nota soltanto al 5%.




Next: Come tener conto degli
Up: Propagazione delle incertezze
Previous: Linearizzazione
Indice
Giulio D'Agostini
2001-04-02
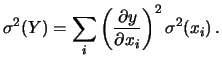
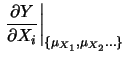 , etc). La derivata di
, etc). La derivata di 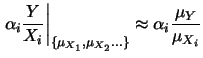 . Questo è equivalente
a moltiplicare la
. Questo è equivalente
a moltiplicare la 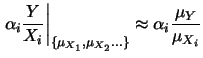 e poi dividere tutto per
e poi dividere tutto per
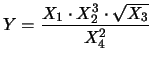 (ad esempio
(ad esempio