



Next: Previsione (o valore atteso)
Up: Variabili casuali e distribuzioni
Previous: Distribuzione geometrica
Indice
Sintesi di una distribuzione di probabilità:
previsione e incertezza di previsione
La distribuzione di probabilità contiene tutte le informazioni
dettagliate sullo stato di incertezza rispetto
al numero aleatorio di interesse,
contenendo, infatti, il nostro grado
di fiducia su ciascuno dei valori che tale numero
può assumere.
Cerchiamo ora di definire delle grandezze
che abbiano la capacità di
riassumere in modo immediato e sintetico alcune
caratteristiche
della distribuzione. Detto alla buona,
esse rispondono alla domanda:
``quali valori ci aspettiamo che si verifichino?''
Prima di mostrare i criteri per definire operativamente
tali grandezze,
aiutiamoci con l'intuito su alcuni esempi, al fine di
capire meglio a quale
domanda ``naturale'' stiamo cercando di rispondere.
Abbiamo visto come, nel caso della distribuzione
geometrica, il valore più probabile non dia l'idea
dei valori che tipicamente si verificano. Lo stesso vale
per l'incertezza di previsione, ovvero per la dispersione
dei valori che si possono ragionevolmente presentare.
Il fatto che per avere
la certezza assoluta bisogna considerare un numero infinito di lanci
non induce ad affermare che ``l'incertezza'' è infinita
e indipendente da  . Come noto, nel caso
del lancio di una moneta, una fluttuazione di
tre o quattro estrazioni, rispetto alle aspettative
di un circa successo ogni due, tende già ad
essere considerata rara.
Nel caso del singolo estratto al lotto invece,
si tendono a considerare
le fluttuazioni ``anomale'' quando il numero di estrazioni
senza successo supera le 50-60. Ciò sta ad indicare
che l'incertezza di previsione è ritenuta, nel secondo
caso,
dell'ordine delle decine di estrazioni.
. Come noto, nel caso
del lancio di una moneta, una fluttuazione di
tre o quattro estrazioni, rispetto alle aspettative
di un circa successo ogni due, tende già ad
essere considerata rara.
Nel caso del singolo estratto al lotto invece,
si tendono a considerare
le fluttuazioni ``anomale'' quando il numero di estrazioni
senza successo supera le 50-60. Ciò sta ad indicare
che l'incertezza di previsione è ritenuta, nel secondo
caso,
dell'ordine delle decine di estrazioni.
Facciamo un esempio con più lanci di una moneta:
- Se lanciamo una moneta 2 volte,
ci aspettiamo che il numero di volte in cui si verifica
testa sarà intorno a 1. Nessuno si stupisce se
esso sarà 0 o 2. Se lanciamo la moneta 1000 volte ci aspettiamo
circa 500 teste, ma riteniamo molto improbabili i valori estremi
di 0 e di 1000. Quindi mentre qualitativamente il primo caso
può essere riassunto in una previsione di
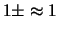 ,
nel secondo caso una previsione di
,
nel secondo caso una previsione di
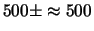 è decisamente pessimistica.
è decisamente pessimistica.
- Nel caso poi che
la moneta venga lanciata invece un numero dispari di volte,
ci ``aspettiamo'' un numero frazionario di successi. Ad esempio
una previsione di 2.5 teste su 5 lanci rende bene l'idea,
anche se nessuno penserà mai di osservare esattamente 2.5 successi!
Ancora degli esempi ispirati alle immancabili urne:
- Considerando
un'urna contente 1000 palline di cui
500 bianche e le restanti nere. Se estraiamo, e successivamente reintroduciamo,
5 palline bianche, le nostre aspettative sul numero di palline bianche
sono analoghe al caso precedente del lancio di una moneta.
In particolare ci aspettiamo che le combinazioni più asimmetriche
(5 bianche o 5 nere) siano le meno probabili. Per ragioni
di simmetria
ci aspettiamo che la probabilità massima sia per
 e
e  .
Quindi un modo alternativo di fornire la previsione potrebbe essere
quello di dire ``i valori che mi aspetto di più sono 2 e 3''.
In particolare, la probabilità che
.
Quindi un modo alternativo di fornire la previsione potrebbe essere
quello di dire ``i valori che mi aspetto di più sono 2 e 3''.
In particolare, la probabilità che  sia
sia 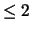 è uguale a
quella di
è uguale a
quella di 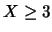 (ne segue che il punto intermedio fra 2 e 3 è quello che
divide i possibili valori di
(ne segue che il punto intermedio fra 2 e 3 è quello che
divide i possibili valori di  in due regioni di pari
probabilità). Quindi anche questi criteri indicherebbero
una previsione dei valori ``fra 2 e 3''.
in due regioni di pari
probabilità). Quindi anche questi criteri indicherebbero
una previsione dei valori ``fra 2 e 3''.
- Si può però immaginare facilmente (il modo standard
di fare i conti sarà mostrato parlando della binomiale)
che cambiando leggermente
la composizione dell'urna (ad esempio 499 bianche, poi 498, 490, etc)
dapprima ci sarà una variazione brusca dell'indicazione
fornita da questa definizione operativa dell'incertezza (nell'esempio
fatto passerà a 2), per diventare poi largamente
insensibile all'esatta composizione dell'urna, per poi
subire un'altra variazione brusca verso il valore 1, e così via.
Riassumendo:
- -
- volendo definire qualitativamente i concetti di
previsione e di incertezza di previsione si può
dire che6.8:
la previsione è un parametro che indica il valore
intorno al quale possa ragionevolmente verificarsi il numero aleatorio;
l'incertezza di previsione è un parametro che
caratterizza la dispersione dei valori che possono essere
ragionevolmente assunti dal numero casuale;
- -
- per quanto concerne la definizione operativa di previsione,
gli esempi hanno mostrato che né il valore
più probabile (chiamato moda) né quello che
divide i possibili valori della variabili in due classi ordinate
di pari probabilità (chiamato mediana) si prestano
a caratterizzare il concetto espresso;
- -
- analogalmente, associare l'incertezza all'ampiezza dell'intervallo
di valori che il numero aleatorio può assumere
conduce a sovrastime
dell'incertezza e ad una insensibilità dal tipo di distribuzione,
sia per variabili definite su un'intervallo finito che infinito.
Inoltre:
- -
- in analogia a parametri che caratterizzano le cosidette
posizione e dispersione dei numeri aleatori,
ce ne sono altre che misurano la forma della distribuzione
in modo più dettagliato di quanto non possa fare l'incertezza
di previsione (legata alla larghezza). Ad esempio, si può
essere interessati al grado di asimmetria della distribuzione
rispetto al suo centro
(vedi paragrafo 6.13).




Next: Previsione (o valore atteso)
Up: Variabili casuali e distribuzioni
Previous: Distribuzione geometrica
Indice
Giulio D'Agostini
2001-04-02
![]() . Come noto, nel caso
del lancio di una moneta, una fluttuazione di
tre o quattro estrazioni, rispetto alle aspettative
di un circa successo ogni due, tende già ad
essere considerata rara.
Nel caso del singolo estratto al lotto invece,
si tendono a considerare
le fluttuazioni ``anomale'' quando il numero di estrazioni
senza successo supera le 50-60. Ciò sta ad indicare
che l'incertezza di previsione è ritenuta, nel secondo
caso,
dell'ordine delle decine di estrazioni.
. Come noto, nel caso
del lancio di una moneta, una fluttuazione di
tre o quattro estrazioni, rispetto alle aspettative
di un circa successo ogni due, tende già ad
essere considerata rara.
Nel caso del singolo estratto al lotto invece,
si tendono a considerare
le fluttuazioni ``anomale'' quando il numero di estrazioni
senza successo supera le 50-60. Ciò sta ad indicare
che l'incertezza di previsione è ritenuta, nel secondo
caso,
dell'ordine delle decine di estrazioni.