



Next: Osservazioni su terminologia e
Up: Variabili casuali e distribuzioni
Previous: Sintesi di una distribuzione
Indice
Previsione (o valore atteso) come baricentro
della distribuzione
Abbiamo visto nel paragrafo 2.14 come il
concetto di previsione (o speranza matematica, o valore atteso) di guadagno
riesca a caratterizzare un problema di decisione
(ad esempio un gioco d'azzardo) senza conoscere i dettagli
del problema (le regole del gioco).
Possiamo estendere questo concetto alle
variabili casuali e definire, in analogia della (2.17),
la previsione di una variabile
casuale
come la somma dei
valori della variabile casuale moltiplicati
per la loro probabilità6.9:
In effetti, non si tratta soltanto di una analogia formale in quanto anche
nel caso della (2.17) si poteva parlare di
numeri aleatori6.10 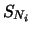 , ciascuno con il suo grado di fiducia
, ciascuno con il suo grado di fiducia 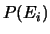 .
Nel seguito preferiremo indicare la previsione con il simbolo
E
.
Nel seguito preferiremo indicare la previsione con il simbolo
E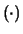 , che ricorda il nome ``valore atteso'' (inglese expected)
e che, trattando ora di variabili casuali, non si confonde più
con il generico simbolo di
evento6.11:
, che ricorda il nome ``valore atteso'' (inglese expected)
e che, trattando ora di variabili casuali, non si confonde più
con il generico simbolo di
evento6.11:
Per capire meglio il significato di
E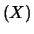 , riscriviamo
la (6.24)
come
, riscriviamo
la (6.24)
come
(operazione consentita in quanto
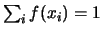 ),
rendendo esplicito il fatto che la previsione di una variabile
casuale rappresenta la media pesata
dei valori delle variabili casuali,
con peso pari alla sua probabilità.
),
rendendo esplicito il fatto che la previsione di una variabile
casuale rappresenta la media pesata
dei valori delle variabili casuali,
con peso pari alla sua probabilità.
Con una espressione mutuata dalla meccanica, possiamo
affermare
che
E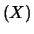 rappresenta il baricentro
della distribuzione di probabilità.
Si riconosce infatti nella (6.25) la coordinata
del centro di massa di un sistema
di punti, ciascuno avente una ``massa di probabilità''
rappresenta il baricentro
della distribuzione di probabilità.
Si riconosce infatti nella (6.25) la coordinata
del centro di massa di un sistema
di punti, ciascuno avente una ``massa di probabilità'' 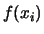 .
Questa constatazione è una ulteriore giustificazione dell'uso
di tale definizione per quantificare il valore intorno al quale
ci aspettiamo che la variabile casuale assuma il valore.
Altre motivazioni che giustificano l'adozione di tale
definizione operativa di previsione verranno indicate nel seguito
(ad esempio
paragrafi 6.5 e 10.7).
.
Questa constatazione è una ulteriore giustificazione dell'uso
di tale definizione per quantificare il valore intorno al quale
ci aspettiamo che la variabile casuale assuma il valore.
Altre motivazioni che giustificano l'adozione di tale
definizione operativa di previsione verranno indicate nel seguito
(ad esempio
paragrafi 6.5 e 10.7).
Prima di passare alle applicazioni, ricordiamo ancora una
volta che il valore atteso non corrisponde, in generale,
né al valore
più probabile, né a uno dei possibili
valori che la variabile casuale può assumere.
Subsections




Next: Osservazioni su terminologia e
Up: Variabili casuali e distribuzioni
Previous: Sintesi di una distribuzione
Indice
Giulio D'Agostini
2001-04-02
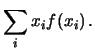
![]() rappresenta il baricentro
della distribuzione di probabilità.
Si riconosce infatti nella (6.25) la coordinata
del centro di massa di un sistema
di punti, ciascuno avente una ``massa di probabilità''
rappresenta il baricentro
della distribuzione di probabilità.
Si riconosce infatti nella (6.25) la coordinata
del centro di massa di un sistema
di punti, ciascuno avente una ``massa di probabilità'' ![]() .
Questa constatazione è una ulteriore giustificazione dell'uso
di tale definizione per quantificare il valore intorno al quale
ci aspettiamo che la variabile casuale assuma il valore.
Altre motivazioni che giustificano l'adozione di tale
definizione operativa di previsione verranno indicate nel seguito
(ad esempio
paragrafi 6.5 e 10.7).
.
Questa constatazione è una ulteriore giustificazione dell'uso
di tale definizione per quantificare il valore intorno al quale
ci aspettiamo che la variabile casuale assuma il valore.
Altre motivazioni che giustificano l'adozione di tale
definizione operativa di previsione verranno indicate nel seguito
(ad esempio
paragrafi 6.5 e 10.7).