



Next: Processo di Poisson -
Up: Distribuzioni di probabilità di
Previous: Usi tipici della distribuzione
Indice
Consideriamo numeri aleatori che seguono distribuzioni
binomiali di parametri 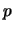 e
e  diversi, ma tali
che il prodotto di
diversi, ma tali
che il prodotto di 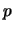 per
per  sia lo stesso, ad esempio
sia lo stesso, ad esempio
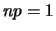 .
Nella tabella 7.1
sono riportate le distribuzioni di probabilità
al variare di
.
Nella tabella 7.1
sono riportate le distribuzioni di probabilità
al variare di 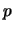 e
e  .
.
Tabella:
Valori della funzione di probabilità di una distribuzione
binomiale al variare di  e
e 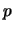 , con il vincolo
, con il vincolo 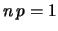 .
Al di sotto di probabilità dello 0.1% è riportato
il solo valore minimo (per
.
Al di sotto di probabilità dello 0.1% è riportato
il solo valore minimo (per  ).
).
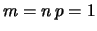 |
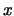 |
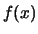 |
| |
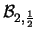 |
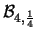 |
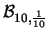 |
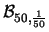 |
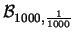 |
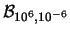 |
| 0 |
0.25 |
0.316 |
0.349 |
0.364 |
0.368 |
0.368 |
| 1 |
0.50 |
0.422 |
0.387 |
0.372 |
0.368 |
0.368 |
| 2 |
0.25 |
0.211 |
0.194 |
0.186 |
0.184 |
0.184 |
| 3 |
|
0.047 |
0.057 |
0.061 |
0.061 |
0.061 |
| 4 |
|
0.004 |
0.011 |
0.015 |
0.015 |
0.015 |
| 5 |
|
|
0.001 |
0.003 |
0.003 |
0.003 |
| 6 |
|
|
... |
... |
0.001 |
... |
| ... |
|
|
... |
... |
... |
... |
| 10 |
|
|
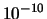 |
... |
... |
... |
| ... |
|
|
|
... |
... |
... |
| 50 |
|
|
|
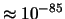 |
... |
... |
| ... |
|
|
|
|
... |
... |
| 1000 |
|
|
|
|
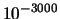 |
... |
| ... |
|
|
|
|
|
... |
| 1000000 |
|
|
|
|
|
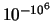 |
|
Si nota innanzitutto che, nonostante  cresca, i valori per
i quali la probabilità è ragionevolmente diversa da zero,
sono soltanto quelli intorno a qualche unità. Inoltre, la distribuzione
sembra stabilizzarsi intorno
a valori di probabilità
che non dipendono dall'esatto valore di
cresca, i valori per
i quali la probabilità è ragionevolmente diversa da zero,
sono soltanto quelli intorno a qualche unità. Inoltre, la distribuzione
sembra stabilizzarsi intorno
a valori di probabilità
che non dipendono dall'esatto valore di  .
Se si facesse una seconda tabella
con un diverso valore di
.
Se si facesse una seconda tabella
con un diverso valore di 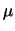 si troverebbe nuovamente un
comportamento asintotico al crescere di
si troverebbe nuovamente un
comportamento asintotico al crescere di  , ovviamente non
alla stessa distribuzione, visto che il valore atteso è diverso.
Quindi al crescere di
, ovviamente non
alla stessa distribuzione, visto che il valore atteso è diverso.
Quindi al crescere di  , la distribuzione sembra dipendere soltanto
da
, la distribuzione sembra dipendere soltanto
da 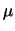 .
.
Questa è una proprietà molto interessante,
in quanto ci sono fenomeni di interesse che sono descritti da leggi
di tipo binomiale, ma con  talmente grande per cui la formula della
distribuzione binomiale sarebbe di scarso uso pratico.
Per esempio supponiamo
di avere un campione di sostanza radioattiva. Il numero di nuclei contenuti
può essere
dell'ordine di
talmente grande per cui la formula della
distribuzione binomiale sarebbe di scarso uso pratico.
Per esempio supponiamo
di avere un campione di sostanza radioattiva. Il numero di nuclei contenuti
può essere
dell'ordine di 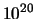 , mentre la probabilità di osservare
un decadimento in un piccolo intervallo di tempo opportunamente
scelto può
essere dell'ordine di
, mentre la probabilità di osservare
un decadimento in un piccolo intervallo di tempo opportunamente
scelto può
essere dell'ordine di 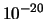 . Il valore atteso del numero di
decadimenti è
. Il valore atteso del numero di
decadimenti è 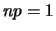 , e quindi ci aspettiamo che la funzione
di probabilità sia la stessa della tabella.
, e quindi ci aspettiamo che la funzione
di probabilità sia la stessa della tabella.
Oltre al vantaggio computazionale appena descritto, è molto
interessante ai fini applicativi che la
distribuzione non dipenda dagli esatti valori di  e di
e di 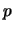 ,
ma solo dal prodotto. Sempre nell'esempio dei decadimenti radioattivi,
i dati sperimentali possono suggerire che il valore atteso di decadimenti
in quell'intervallo di tempo sia 1. È allora possibile valutare
la distribuzione di probabilità senza conoscere né
,
ma solo dal prodotto. Sempre nell'esempio dei decadimenti radioattivi,
i dati sperimentali possono suggerire che il valore atteso di decadimenti
in quell'intervallo di tempo sia 1. È allora possibile valutare
la distribuzione di probabilità senza conoscere né
 né
né 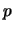 , stante
la sola ragionevolissima condizione che
, stante
la sola ragionevolissima condizione che  sia ``grande''.
sia ``grande''.
Per dimostrare che quanto mostrato nella tabella è una
proprietà generale,
facciamo il limite della distribuzione binomiale per
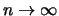 e
e
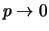 , con la condizione che
, con la condizione che
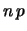 resti finito e molto minore di
resti finito e molto minore di  .
Indichiamo7.2
il prodotto
.
Indichiamo7.2
il prodotto 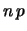 con
con 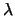 .
Riscriviamo la formula della distribuzione binomiale:
.
Riscriviamo la formula della distribuzione binomiale:
Sostituendo a 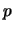 si vede che fare il limite
si vede che fare il limite
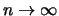 e
e
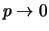 corrisponde al solo limite
corrisponde al solo limite
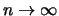 , ovvero:
Mettendo a fattore i termini non dipendenti da
, ovvero:
Mettendo a fattore i termini non dipendenti da  e
riscrivendo il rapporto fra
e
riscrivendo il rapporto fra 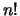 e
e 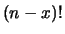 nella sua
forma originaria, cioè
nella sua
forma originaria, cioè
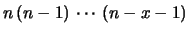 riscriviamo il limite di
riscriviamo il limite di 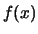 come:
Notiamo che, per tale limite:
come:
Notiamo che, per tale limite:
- il numeratore della seconda frazione è uguale a
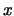 fattori, ciascuno
circa uguale a
fattori, ciascuno
circa uguale a  , in quanto
, in quanto 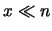 ; esso è quindi uguale al
denominatore e si semplifica;
; esso è quindi uguale al
denominatore e si semplifica;
- il numeratore della terza frazione tende, come noto,
a
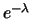 ;
;
- il denominatore della terza frazione tende a 1.
In conclusione abbiamo:
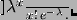
(finito)
![$\displaystyle \end{array}]{}\frac{\lambda^x}{x!}\, e^{-\lambda}\,.
$](img1369.png)
Otteniamo quindi una distribuzione di probabilità caratterizzata dal
solo parametro 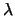 , numero reale positivo,
chiamata distribuzione
di Poisson o (poissoniana),
che indichiamo nel seguente modo
, numero reale positivo,
chiamata distribuzione
di Poisson o (poissoniana),
che indichiamo nel seguente modo
 |
(7.8) |
Non c'è bisogno di calcolare il valore atteso e la varianza della
distribuzione,7.3
in quanto possono essere ottenute dalla binomiale
effettuando il limite per
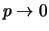 . Ne segue:
. Ne segue:
Riportiamo nella tabella
7.2
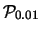 per
alcuni valori (piccoli) di
per
alcuni valori (piccoli) di 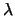 .
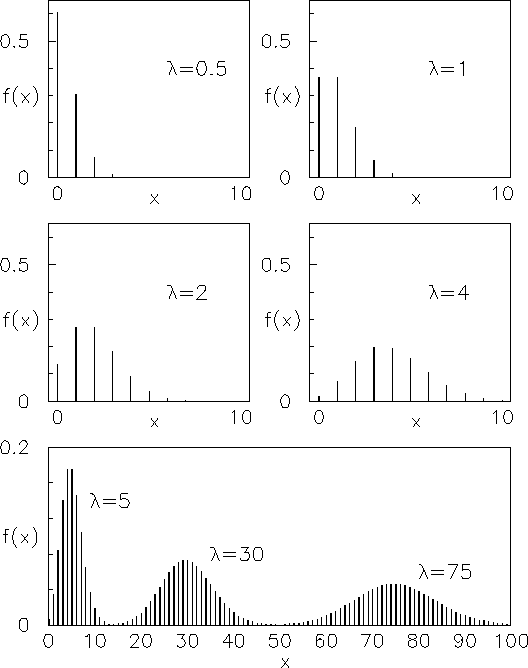
La figura 7.2 mostra alcuni esempi di
rappresentazione grafica.
.
La figura 7.2 mostra alcuni esempi di
rappresentazione grafica.
Tabella:
Distribuzione di Poisson per alcuni
valori di 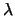 . Gli eventi di massima probabilità sono
indicati in grassetto.
. Gli eventi di massima probabilità sono
indicati in grassetto.
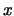 |
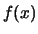 |
| |
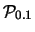 |
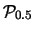 |
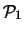 |
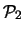 |
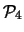 |
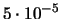 |
| 0 |
0.990 |
0.905 |
0.607 |
0.368 |
0.135 |
0.018 |
| 1 |
0.010 |
0.090 |
0.303 |
0.368 |
0.271 |
0.073 |
| 2 |
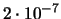 |
0.005 |
0.076 |
0.184 |
0.271 |
0.147 |
| 3 |
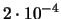 |
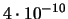 |
0.013 |
0.061 |
0.180 |
0.195 |
| 4 |
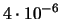 |
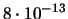 |
0.002 |
0.015 |
0.090 |
0.195 |
| 5 |
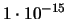 |
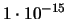 |
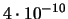 |
0.003 |
0.036 |
0.156 |
| 6 |
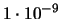 |
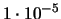 |
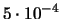 |
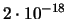 |
0.012 |
0.104 |
| 7 |
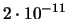 |
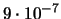 |
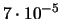 |
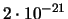 |
0.003 |
0.060 |
| 8 |
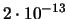 |
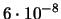 |
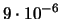 |
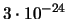 |
0.001 |
0.030 |
| 9 |
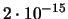 |
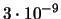 |
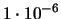 |
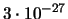 |
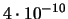 |
0.015 |
| 10 |
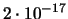 |
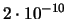 |
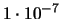 |
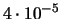 |
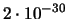 |
0.005 |
| 11 |
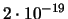 |
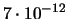 |
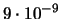 |
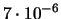 |
 |
0.002 |
|
Figura:
Esempi di distribuzione di Poisson con 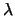 uguale
a 0.5, 1, 2, 4, 5, 30 e 75 (le ultime tre sono sovrapposte
nel grafico in basso).
uguale
a 0.5, 1, 2, 4, 5, 30 e 75 (le ultime tre sono sovrapposte
nel grafico in basso).
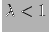 |
Si noti come la
probabilità di osservare  sia data da
sia data da
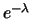 .
Per
.
Per
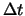 essa è chiaramente dominante e diventa
trascurabile soltanto per
essa è chiaramente dominante e diventa
trascurabile soltanto per 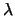 abbastanza grande.
Al crescere di
abbastanza grande.
Al crescere di 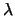 la distribuzione comincia
a diventare simmetrica intorno al valor medio, il quale si avvicina anche al
valore di massima probabilità.
la distribuzione comincia
a diventare simmetrica intorno al valor medio, il quale si avvicina anche al
valore di massima probabilità.




Next: Processo di Poisson -
Up: Distribuzioni di probabilità di
Previous: Usi tipici della distribuzione
Indice
Giulio D'Agostini
2001-04-02
![]() cresca, i valori per
i quali la probabilità è ragionevolmente diversa da zero,
sono soltanto quelli intorno a qualche unità. Inoltre, la distribuzione
sembra stabilizzarsi intorno
a valori di probabilità
che non dipendono dall'esatto valore di
cresca, i valori per
i quali la probabilità è ragionevolmente diversa da zero,
sono soltanto quelli intorno a qualche unità. Inoltre, la distribuzione
sembra stabilizzarsi intorno
a valori di probabilità
che non dipendono dall'esatto valore di ![]() .
Se si facesse una seconda tabella
con un diverso valore di
.
Se si facesse una seconda tabella
con un diverso valore di ![]() si troverebbe nuovamente un
comportamento asintotico al crescere di
si troverebbe nuovamente un
comportamento asintotico al crescere di ![]() , ovviamente non
alla stessa distribuzione, visto che il valore atteso è diverso.
Quindi al crescere di
, ovviamente non
alla stessa distribuzione, visto che il valore atteso è diverso.
Quindi al crescere di ![]() , la distribuzione sembra dipendere soltanto
da
, la distribuzione sembra dipendere soltanto
da ![]() .
.
![]() talmente grande per cui la formula della
distribuzione binomiale sarebbe di scarso uso pratico.
Per esempio supponiamo
di avere un campione di sostanza radioattiva. Il numero di nuclei contenuti
può essere
dell'ordine di
talmente grande per cui la formula della
distribuzione binomiale sarebbe di scarso uso pratico.
Per esempio supponiamo
di avere un campione di sostanza radioattiva. Il numero di nuclei contenuti
può essere
dell'ordine di ![]() , mentre la probabilità di osservare
un decadimento in un piccolo intervallo di tempo opportunamente
scelto può
essere dell'ordine di
, mentre la probabilità di osservare
un decadimento in un piccolo intervallo di tempo opportunamente
scelto può
essere dell'ordine di ![]() . Il valore atteso del numero di
decadimenti è
. Il valore atteso del numero di
decadimenti è ![]() , e quindi ci aspettiamo che la funzione
di probabilità sia la stessa della tabella.
, e quindi ci aspettiamo che la funzione
di probabilità sia la stessa della tabella.
![]() e di
e di ![]() ,
ma solo dal prodotto. Sempre nell'esempio dei decadimenti radioattivi,
i dati sperimentali possono suggerire che il valore atteso di decadimenti
in quell'intervallo di tempo sia 1. È allora possibile valutare
la distribuzione di probabilità senza conoscere né
,
ma solo dal prodotto. Sempre nell'esempio dei decadimenti radioattivi,
i dati sperimentali possono suggerire che il valore atteso di decadimenti
in quell'intervallo di tempo sia 1. È allora possibile valutare
la distribuzione di probabilità senza conoscere né
![]() né
né ![]() , stante
la sola ragionevolissima condizione che
, stante
la sola ragionevolissima condizione che ![]() sia ``grande''.
sia ``grande''.
![]() e
e
![]() , con la condizione che
, con la condizione che
![]() resti finito e molto minore di
resti finito e molto minore di ![]() .
Indichiamo7.2
il prodotto
.
Indichiamo7.2
il prodotto ![]() con
con ![]() .
Riscriviamo la formula della distribuzione binomiale:
.
Riscriviamo la formula della distribuzione binomiale:
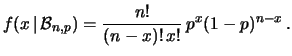
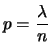
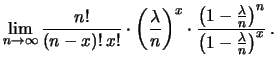
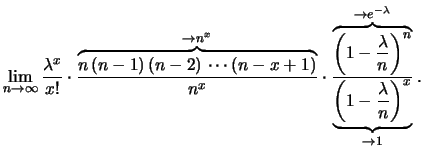
![$\displaystyle \end{array}]{}\frac{\lambda^x}{x!}\, e^{-\lambda}\,.
$](img1369.png)