



Next: pzd100 Formule ricorsive per
Up: Distribuzioni di probabilità di
Previous: Distribuzione di Poisson
Indice
 Processo di Poisson -
prima parte
Processo di Poisson -
prima parte
La distribuzione di Poisson è stata introdotta nel paragrafo
precedente come limite della distribuzione binomiale. Per quanto
riguarda l'interpretazione fisica dei parametri  e
e  , suggerita
anche dall'esempio sui decadimenti radioattivi, si può pensare che:
, suggerita
anche dall'esempio sui decadimenti radioattivi, si può pensare che:
- -
 sia il numero di ``oggetti'' ai quali può
succedere qualcosa;
sia il numero di ``oggetti'' ai quali può
succedere qualcosa;
- -
 sia la probabilità che a ciascuno di quelli eventi succeda
``quella cosa''. Essa è la stessa per tutti gli
sia la probabilità che a ciascuno di quelli eventi succeda
``quella cosa''. Essa è la stessa per tutti gli  oggetti.
oggetti.
Questo punto di vista può essere per alcuni aspetti limitativo,
in quanto non sempre è possibile o ha senso
tale schematizzazione. Se ad esempio pensiamo
alla probabilità che una macchina rossa percorra un tratto di strada
in un certo intervallo di tempo, una trattazione
secondo la distribuzione di Poisson
implicherebbe una precedente schematizzazione in termini
binomiali, con  pari al numero di macchine e
pari al numero di macchine e  la probabilità
che ciascuna delle macchine transiti a quell'ora. Ma bisognerà considerare
solo le macchine di quella città o ``tutte'' le macchine?
E poi anche
la probabilità
che ciascuna delle macchine transiti a quell'ora. Ma bisognerà considerare
solo le macchine di quella città o ``tutte'' le macchine?
E poi anche  varia da macchina a macchina! Volendo si può anche
risolvere il problema insistendo a voler riferire
varia da macchina a macchina! Volendo si può anche
risolvere il problema insistendo a voler riferire  alle macchine
e intendendo
alle macchine
e intendendo  una probabilità condizionata dalla sola conoscenza
di ``macchina rossa'' (una sorta di
una probabilità condizionata dalla sola conoscenza
di ``macchina rossa'' (una sorta di  media).
media).
È interessante
mostrare lo stesso problema da un altro punto di vista,
quello degli atti elementari di osservazione.
Questo modo alternativo di ragionare è
molto più generale del precedente ed inoltre collega il numero aleatorio
``numero di osservazioni'' al numero aleatorio reale ``tempo fra due
osservazioni successive'' (questo secondo aspetto verrà
ripreso nel paragrafo ![[*]](file:/usr/lib/latex2html/icons/crossref.png) )
)
Consideriamo fenomeni che si manifestano nel tempo
o nello spazio e di cui siamo interessanti al numero di occorrenze,
indipendentemente dall'ordine. Si parla in generale di
misure di conteggio. Esempi tipici sono
- -
- telefonate che arrivano ad un centralino;
- -
- errori di stampa in un libro;
- -
- decadimenti radioattivi in un tempo molto
inferiore a quello di dimezzamento;
- -
- numero di globuli bianchi osservati al microscopio
in un campo ottico;
- -
- difetti di fabbricazione di un cavo;
- -
- numero di molecole in un piccolo volume di gas;
Ciascuno di questi fenomeni può manifestarsi,
indipendentemente dagli altri, in un certo intervallo o elemento
molto piccolo, sia esso di tempo, lunghezza, superficie o volume
(rispettivamente
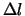 ,
,
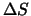 ,
,
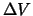 e
e
 ).
).
Figura:
Processo di Poisson nel dominio del tempo. Le
crocette indicano gli istanti delle occorrenze delle osservazioni.
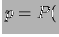 |
Nel seguito, per comodità ma senza perdere di generalità,
prenderemo in considerazione problemi nel dominio del tempo
(vedi figura 7.3)
Interessiamoci quindi al numero di conteggi
registrati in un certo intervallo finito di tempo  ,
ovvero il numero aleatorio è
definito come
,
ovvero il numero aleatorio è
definito come  = ``numero di conteggi fra 0 e
= ``numero di conteggi fra 0 e  ''.
Supponiamo ora che
''.
Supponiamo ora che
- La probabilità che che si verifichi esattamente un conteggio
in un intervallino
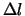 sia proporzionale a
sia proporzionale a 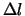 :
con
:
con  costante nell'intervallo finito
costante nell'intervallo finito  , in modo tale che
, in modo tale che
 non dipenda dall'intervallino preso in considerazione,
ma soltanto dalla sua sola durata;
non dipenda dall'intervallino preso in considerazione,
ma soltanto dalla sua sola durata;
- La probabilità che in
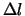 si verifichino più
di 1 eventi sia trascurabile in confronto a quella che
se ne verifichi esattamente 1;
si verifichino più
di 1 eventi sia trascurabile in confronto a quella che
se ne verifichi esattamente 1;
- il numero di conteggi in un intervallo finito
sia indipendente dal numero di conteggi che si verificano in un altro
intervallo, se i due intervalli sono disgiunti.
Queste ipotesi definiscono i cosidetti processi di Poisson.
Consideriamo  intervallini disgiunti, ciascuno
di durata
intervallini disgiunti, ciascuno
di durata 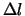 , tali che
, tali che
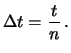 , ovvero
, ovvero
Quando  tende ad infinito ne segue che
tende ad infinito ne segue che
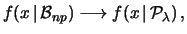 e, di conseguenza,
e, di conseguenza,
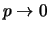 .
Consideriamo inoltre che:
con
Essendo il valore atteso della
distribuzione di Poisson uguale a
.
Consideriamo inoltre che:
con
Essendo il valore atteso della
distribuzione di Poisson uguale a 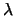 , e quest'ultima
pari a
, e quest'ultima
pari a 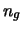 , si vede quindi che
, si vede quindi che  ha il
significato di numero atteso di conteggi per unità di tempo,
ovvero quantifica l'intensità del processo.
Il simbolo
ha il
significato di numero atteso di conteggi per unità di tempo,
ovvero quantifica l'intensità del processo.
Il simbolo  dovrebbe ricordare il ``rateo'' (tasso), in inglese
``rate''(e, in una tipica applicazione di tale processo, anche
la radioattività).
dovrebbe ricordare il ``rateo'' (tasso), in inglese
``rate''(e, in una tipica applicazione di tale processo, anche
la radioattività).
Come già detto, alcuni problemi possono essere considerati
o dal punto di vista degli  oggetti o dal punto di vista
degli
oggetti o dal punto di vista
degli  atti di osservazione. Consideriamo i due casi
per mostrare che il numero aleatorio ``globuli nel sangue
osservati al microscopio'' segue una distribuzione di Poisson:
atti di osservazione. Consideriamo i due casi
per mostrare che il numero aleatorio ``globuli nel sangue
osservati al microscopio'' segue una distribuzione di Poisson:
- A)
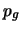 :
:- numero di globuli di una persona;
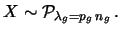 :
:- probabilità che un certo globulo venga estratto
e che si trovi nel campo ottico di quella osservazione.
Essendo 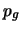 molto grande e
molto grande e 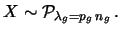 molto piccolo,
ne segue che
molto piccolo,
ne segue che
- B)
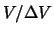 :
:- numero di volumetti (
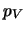 ) di cui è costituito
il sangue nel campo del microscopio;
) di cui è costituito
il sangue nel campo del microscopio;
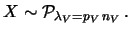 :
:- probabilità di trovare un globulo in un
volumetto
 ;
;
Anche in questo caso 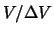 è molto grande, in quanto
è molto grande, in quanto  può essere pensato dell'ordine di grandezza del globulo stesso.
Ne segue che
può essere pensato dell'ordine di grandezza del globulo stesso.
Ne segue che
È da notare come  e
e  siano
diversi nei due casi (e di conseguenza
sono stati designati con simboli diversi), ma la distribuzione risultante
è la stessa (
siano
diversi nei due casi (e di conseguenza
sono stati designati con simboli diversi), ma la distribuzione risultante
è la stessa (
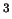 ), in quanto
essa dipende soltanto dal valore atteso di conteggi e non da
), in quanto
essa dipende soltanto dal valore atteso di conteggi e non da
 e da
e da  separatamente.
separatamente.
Terminiamo con due osservazioni,
una relativa all'uso
della distribuzione di Poisson, l'altra sui cosidetti ``eventi rari''.
Innanzitutto è importante ricordare che gli oggetti da
contare debbano apparire
indipendentemente uno dall'altro. Per esempio, se alcuni
oggetti preferiscono manifestarsi a coppie o a gruppi più numerosi
(per esempio i turisti giapponesi su un autobus) non si
può applicare la distribuzione di Poisson sui singoli elementi,
ma eventualmente sui gruppi, se si crede
che essi sono siano loro indipendenti (sicuramente non vale per
i gruppi di turisti, schedulati dalle agenzie di viaggio...).
Talvolta la distribuzione di Poisson è chiamata
anche ``distribuzione degli eventi rari''.
Questo può essere giustificato dal fatto che
nell'intervallino dell'atto di elementare osservazione
la probabilità è effettivamente bassa
(o simmetricamente che sia molto bassa la probabilità che
a ciascuno degli oggetti in questione possa
succedere qualcosa),
oppure perché in molti
casi macroscopici la ``rarità'' del fenomeno è richiesta
dalla condizione di indipendenza degli eventi (gli affollamenenti
creano inevitabilmente delle correlazioni: ad esempio il numero di
macchine che transitano per una strada di campagna fra
le 10 e le 11 del mattino può essere descritto da un processo di Poisson,
ma sicuramente tale schematizzazione non può andare bene per
descrivere il traffico urbano nelle ore di punta).
Ma queste condizioni non implicano che tutti gli eventi debbano
essere ``rari'' su scala umana. Ad esempio un materiale radiattivo
potrebbe emettere un milione di particelle al secondo, oppure
si può essere interessati al numero di molecole contenute in un
cm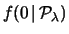 di aria, ottenendo previsioni tutt'altro che
piccole pur essendo tali numeri aleatori ben descritti
da distribuzioni di Poisson.
di aria, ottenendo previsioni tutt'altro che
piccole pur essendo tali numeri aleatori ben descritti
da distribuzioni di Poisson.




Next: pzd100 Formule ricorsive per
Up: Distribuzioni di probabilità di
Previous: Distribuzione di Poisson
Indice
Giulio D'Agostini
2001-04-02
![]() )
)
![]() intervallini disgiunti, ciascuno
di durata
intervallini disgiunti, ciascuno
di durata ![]() , tali che
, tali che
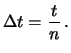 , ovvero
, ovvero
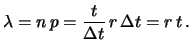
![]() oggetti o dal punto di vista
degli
oggetti o dal punto di vista
degli ![]() atti di osservazione. Consideriamo i due casi
per mostrare che il numero aleatorio ``globuli nel sangue
osservati al microscopio'' segue una distribuzione di Poisson:
atti di osservazione. Consideriamo i due casi
per mostrare che il numero aleatorio ``globuli nel sangue
osservati al microscopio'' segue una distribuzione di Poisson:
![]() di aria, ottenendo previsioni tutt'altro che
piccole pur essendo tali numeri aleatori ben descritti
da distribuzioni di Poisson.
di aria, ottenendo previsioni tutt'altro che
piccole pur essendo tali numeri aleatori ben descritti
da distribuzioni di Poisson.