



Next: Variabili casuali - II
Up: Distribuzioni di probabilità di
Previous: Ricapitolando
Indice
- Una variabile casuale,
definita nell'intervallo [0,4] segue una distribuzione uniforme.
Quanto vale la probabilità che su 3 realizzazioni della
variabile casuale nessuna sia maggiore di
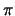 ?
?
- Una variabile casuale, definita fra 0 e 1 ha una densità
di probabilità proporzionale al valore della variabile.
Trovare la forma della distribuzione, il valore medio e la
deviazione standard.
- Dalla definizione di variabile normale standardizzata
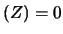 e dalle proprietà del valore aspettato e della
varianza dimostrare che
E
e dalle proprietà del valore aspettato e della
varianza dimostrare che
E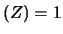 e
Var
e
Var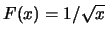 .
.
- Una variabile casuale continua
ha la seguente funzione di ripartizione
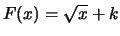 . Sapendo che il valore minimo che
la variabile può assumere è 1, quanto vale il valore massimo?
Quanto vale il valor medio e la
deviazione standard della distribuzione?
. Sapendo che il valore minimo che
la variabile può assumere è 1, quanto vale il valore massimo?
Quanto vale il valor medio e la
deviazione standard della distribuzione?
- Risolvere il problema precedente nel caso
in cui sia
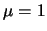 .
.
- Una variabile casuale segue una distribuzione normale di
parametri
 e
e 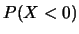 . Calcolare:
. Calcolare: 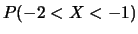 ;
;
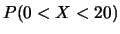 ;
;
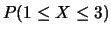 ;
;
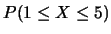 ;
;
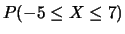 ;
;
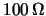 .
.
- Una ditta produce resistori da
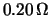 . Da campionamenti effettuati
in periodi diversi e sotto diverse condizioni di lavoro delle macchine
e di forniture dei materiali risulta che i valori delle resistenza
dei singoli campioni sono
centrati intorno al valore nominale con distribuzione gaussiana
di deviazione standard
. Da campionamenti effettuati
in periodi diversi e sotto diverse condizioni di lavoro delle macchine
e di forniture dei materiali risulta che i valori delle resistenza
dei singoli campioni sono
centrati intorno al valore nominale con distribuzione gaussiana
di deviazione standard
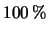 . Qual'è la percentuale
di resistori il cui valore si discosta di più dell'1%
dal valore nominale?
. Qual'è la percentuale
di resistori il cui valore si discosta di più dell'1%
dal valore nominale?
- Calcolare media e deviazione standard di una distribuzione
esponenziale mediante la funzione generatrice dei
momenti. *** prossimo capitolo ***
- In un paese il reddito per ogni persona è pari a 10000$
l'anno
con una deviazione standard di 3000$. Qual'è la percentuale
di persone che hanno un reddito superiore a 30000$?
- Una variabile è distribuita normalmente intorno al valore medio
di 30. Sapendo che la probabilità che la variabile
ecceda il valore di
50 è del
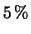 , quanto vale la probabilità di avere un valore
inferiore a 20?
, quanto vale la probabilità di avere un valore
inferiore a 20?
- Calcolare media e deviazione standard di una distribuzione
esponenziale mediante la funzione generatrice dei
momenti.
- La radioattività dovuta ad un campione di di materiale produce
su un opportuno strumento,
in grado di rivelare le particelle dovute a ciascun
decadimento con il
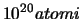 di probabilità,
15 conteggi al minuto. Sapendo che il campione contiene
di probabilità,
15 conteggi al minuto. Sapendo che il campione contiene
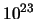 ,
determinare la vita media del nucleo di tale sostanza.
Supponiamo che i protoni e i nucleoni8.6
abbiano una vita media di
10 miliardi di anni, ovvero dell'ordine di grandezza
dell'età dell'Universo. Stimare il valore della radiattività, misurata
in conteggi al secondo, emessa da una persona di
,
determinare la vita media del nucleo di tale sostanza.
Supponiamo che i protoni e i nucleoni8.6
abbiano una vita media di
10 miliardi di anni, ovvero dell'ordine di grandezza
dell'età dell'Universo. Stimare il valore della radiattività, misurata
in conteggi al secondo, emessa da una persona di 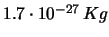 .
(Si ricorda che protoni circa la stessa massa, pari a
.
(Si ricorda che protoni circa la stessa massa, pari a
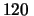 , e che la massa dovuta agli elettroni è trascurabile.).
, e che la massa dovuta agli elettroni è trascurabile.).




Next: Variabili casuali - II
Up: Distribuzioni di probabilità di
Previous: Ricapitolando
Indice
Giulio D'Agostini
2001-04-02