



Next: Trasformazioni di una distribuzione
Up: pzd100Soluzione generale per variabili
Previous: pzd100Soluzione generale per variabili
Indice
Prendiamo la variabile  , con funzione densità di probabilità
, con funzione densità di probabilità
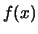 , e consideriamo una funzione
crescente
, e consideriamo una funzione
crescente 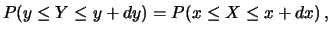 . Applicando quanto appena
espresso a parole per il caso generale,
abbiamo che
. Applicando quanto appena
espresso a parole per il caso generale,
abbiamo che
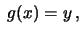
con
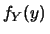
ovvero
in cui è stato esplicitato il fatto (generalmente sottinteso in questo
testo) che
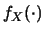 è una funzione di
è una funzione di 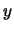 mentre
mentre
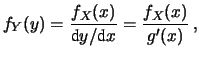 è funzione di
è funzione di  .
Ne segue che
.
Ne segue che
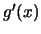 |
(10.11) |
dove con
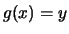 è stata indicata la derivata di
è stata indicata la derivata di 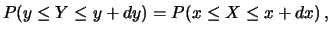 calcolata in corrispondenza di
calcolata in corrispondenza di  tale che
tale che 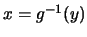 ,
ovvero di
,
ovvero di
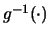 , ove - chiariamo -
(
, ove - chiariamo -
(
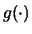 sta per la funzione inversa di
sta per la funzione inversa di 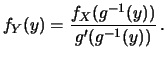 .
Quindi il modo più corretto per esprimere la (10.11),
funzione solo di
.
Quindi il modo più corretto per esprimere la (10.11),
funzione solo di 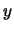 , è
, è
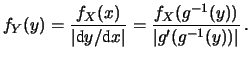 |
(10.12) |
Nel caso che 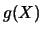 sia decrescente si segue un ragionamento analogo,
ma nel risultato finale cambia il segno al secondo membro. Quindi
la formula generale, per funzioni sempre crescenti o sempre decrescenti
è:
sia decrescente si segue un ragionamento analogo,
ma nel risultato finale cambia il segno al secondo membro. Quindi
la formula generale, per funzioni sempre crescenti o sempre decrescenti
è:
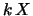 |
(10.13) |
Ad esempio, se la trasformazione è del tipo 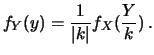 , si ottiene
Vediamo in dettaglio cosa succede quando si applica una
trasformazione ad una variabile distribuita uniformemente.
, si ottiene
Vediamo in dettaglio cosa succede quando si applica una
trasformazione ad una variabile distribuita uniformemente.
Subsections




Next: Trasformazioni di una distribuzione
Up: pzd100Soluzione generale per variabili
Previous: pzd100Soluzione generale per variabili
Indice
Giulio D'Agostini
2001-04-02
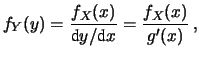 è funzione di
è funzione di 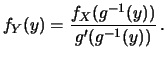 .
Quindi il modo più corretto per esprimere la (10.11),
funzione solo di
.
Quindi il modo più corretto per esprimere la (10.11),
funzione solo di 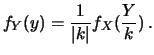 , si ottiene
, si ottiene