



Next: Applicazioni alle simulazioni di
Up: Cambiamento di variabile
Previous: Cambiamento di variabile
Indice
Il caso della distribuzione di partenza uniforme è interessante
in quanto esso mostra chiaramente
la distorsione delle funzioni densità
di probabilità operate dal cambiamento di metrica. Questo
si capisce meglio se si osserva attentamente la figura
10.2, in cui le diverse densità dei puntini
danno un'idea della funzione densità di probabilità.
È anche interessante confrontare quanto ottenuto
con la discussione fatta
a proposito delle
trasformazioni uniformi variabili discrete (vedi anche tabella
10.1).
Figura:
Esempi di trasformazione di variabile; A)
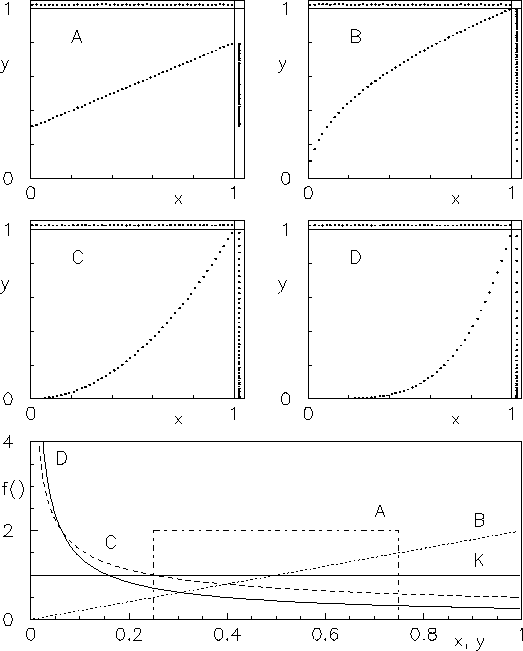 ;
B)
;
B) 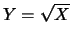 ; C)
; C) 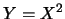 ; D)
; D)  .
.
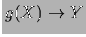 |
Le funzioni 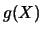 utilizzate e la funzione densità di probabilità
delle trasformate sono date in
tabella 10.2.
I calcoli vengono lasciati per
esercizio.
utilizzate e la funzione densità di probabilità
delle trasformate sono date in
tabella 10.2.
I calcoli vengono lasciati per
esercizio.
Tabella:
Funzioni densità di probabilità ottenute da diverse
trasformazioni di una variabile distribuita uniformemente fra 0 e 1.
|
.
|




Next: Applicazioni alle simulazioni di
Up: Cambiamento di variabile
Previous: Cambiamento di variabile
Indice
Giulio D'Agostini
2001-04-02
![]() utilizzate e la funzione densità di probabilità
delle trasformate sono date in
tabella 10.2.
I calcoli vengono lasciati per
esercizio.
utilizzate e la funzione densità di probabilità
delle trasformate sono date in
tabella 10.2.
I calcoli vengono lasciati per
esercizio.