



Next: Indipendenza stocastica (o in
Up: Regole della probabilità
Previous: Relazione fra probabilità condizionata
Indice
Il fatto che la formula (4.17)
non possa definire
la probabilità condizionata, ma ne offra soltanto una valutazione
se sono noti gli altri due termini,
può essere compreso,
oltre che dai ragionamenti di buon senso fatti precedentemente,
dal considerare gli eventi di probabilità nulla nel senso chiarito
nel paragrafo 2.7.
Innanzitutto è chiaro che
la probabilità di un evento condizionato con sé stesso
deve essere sempre uguale ad uno, indipendentemente
dal valore di 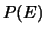 ,
in quanto
,
in quanto
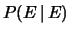 rappresenta ``la probabilità di
rappresenta ``la probabilità di  nell'ipotesi
che
nell'ipotesi
che  sia vero'':
sia vero'':
Inoltre, se consideriamo due eventi  e
e  di probabilità nulla, ma
ai quali attribuiamo lo stesso grado di fiducia (si considerino ad esempio
le condizioni ``normali'' di traffico descritte nel
paragrafo 2.7) deve valere:
di probabilità nulla, ma
ai quali attribuiamo lo stesso grado di fiducia (si considerino ad esempio
le condizioni ``normali'' di traffico descritte nel
paragrafo 2.7) deve valere:
sebbene queste probabilità non siano ottenibili
dalla (4.17).
Gli esempi appena riportati possono
sembrare più delle curiosità che dei
casi di interesse scientifico. È invece facile convincersi,
ad esempio, che
ogni volta che si valuta la probabilità di qualche evento mediante
simulazioni al computer che dipendono da parametri rispetto
ai quali si è in condizione di incertezza si sta usando esattamente
il concetto di condizionamento da eventi di probabilità nulla.




Next: Indipendenza stocastica (o in
Up: Regole della probabilità
Previous: Relazione fra probabilità condizionata
Indice
Giulio D'Agostini
2001-04-02
![]() ,
in quanto
,
in quanto
![]() rappresenta ``la probabilità di
rappresenta ``la probabilità di ![]() nell'ipotesi
che
nell'ipotesi
che ![]() sia vero'':
sia vero'':