



Next: Altre proprietà della probabilità
Up: Regole della probabilità
Previous: Condizionamento da eventi di
Indice
Immaginiamo l'esperimento del lancio di
due dadi regolari distinguibili e di indicare con 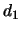 e
e 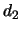 i rispettivi valori. Interessiamoci alla probabilità dei
seguenti eventi
relativi al
i rispettivi valori. Interessiamoci alla probabilità dei
seguenti eventi
relativi al 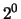 dado
dado
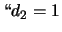 ''
''
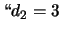 '' e
'' e 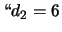 ''. Per simmetria possiamo solo assegnare
probabilità 1/6 a ciascuno degli eventi. Consideriamo ora di voler
valutare la probabilità nell'ipotesi che i seguenti eventi siano
alternativamente veri:
''. Per simmetria possiamo solo assegnare
probabilità 1/6 a ciascuno degli eventi. Consideriamo ora di voler
valutare la probabilità nell'ipotesi che i seguenti eventi siano
alternativamente veri: 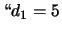 '';
'';
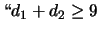 '';
'';
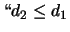 ''.
(Una persona potrebbe sbirciare il risultato e darci queste informazioni.)
''.
(Una persona potrebbe sbirciare il risultato e darci queste informazioni.)
Figura:
Spazio campionario ed esempi di eventi nel caso di lancio
di due dadi. Sono indicati i condizionamenti ``la somma è maggiore o uguale
a 9'' e ``il secondo valore è non superiore al primo''.
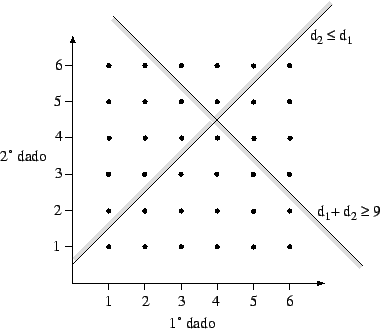 |
Calcolando direttamente4.5le probabilità condizionate facendo uso
della figura 4.3 otteniamo per i tre condizionamenti:
Si vede quindi come il nuovo stato di informazione possa
aumentare, diminuire o inalterare la credibilità dell'evento
in considerazione. Anche chi non sa - o non ha tempo di -
fare i conti in dettaglio
intuisce come, se la somma dei due risultati è maggiore o uguale a
9, sia più facile che
si verifichino valori alti per il secondo dado,
e sicuramente non inferiori a 3.
Se l'ipotesi che un evento 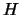 sia vero cambia la probabilità
di un altro evento (
sia vero cambia la probabilità
di un altro evento ( ) diciamo che i due eventi sono correlati:
) diciamo che i due eventi sono correlati:
- se
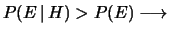
 e
e 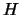 sono correlati
positivamente;
sono correlati
positivamente;
- se
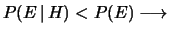
 e
e 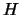 sono correlati
negativamente.
sono correlati
negativamente.
Altrimenti
- se
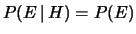 i due eventi sono indipendenti, o più
propriamente indipendenti in probabilità (o stocasticamente
indipendenti).
i due eventi sono indipendenti, o più
propriamente indipendenti in probabilità (o stocasticamente
indipendenti).
In questo caso il teorema delle probabilità composte diventa:
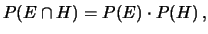 |
(4.21) |
nota come regola della moltiplicazione della probabilità di
eventi indipendenti.
Questa relazione può essere
un modo alternativo alla condizione
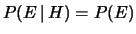 per definire
l'indipendenza stocastica.
Si noti come l'uso della
(4.21) sia duplice. Ci sono dei casi in
cui è possibile valutare direttamente i tre termini della relazione
e verificare l'indipendenza, oppure assumere l'indipendenza
e utilizzare tale formula per calcolare la probabilità congiunta
a partire dalle probabilità dei due eventi
(o in genere del terzo incognito).
per definire
l'indipendenza stocastica.
Si noti come l'uso della
(4.21) sia duplice. Ci sono dei casi in
cui è possibile valutare direttamente i tre termini della relazione
e verificare l'indipendenza, oppure assumere l'indipendenza
e utilizzare tale formula per calcolare la probabilità congiunta
a partire dalle probabilità dei due eventi
(o in genere del terzo incognito).




Next: Altre proprietà della probabilità
Up: Regole della probabilità
Previous: Condizionamento da eventi di
Indice
Giulio D'Agostini
2001-04-02


![$\displaystyle \left\{\! \begin{array}{l}
P(d_2=1\,\vert\,d_1=5) = 1/6 \hspace{1...
...\
P(d_2=6\,\vert\,d_1=5) = 1/6 \hspace{1.23 cm}[= P(d_2=6)]
\end{array}\right.$](img670.png)
![$\displaystyle \left\{\! \begin{array}{l}
P(d_2=1\,\vert\,d_1+d_2\ge 9) = 0 \hsp...
...2=6\,\vert\,d_1+d_2\ge 9) = 4/10 \hspace{0.2 cm}[> P(d_2=6)]
\end{array}\right.$](img672.png)
![$\displaystyle \left\{\! \begin{array}{l}
P(d_2=1\,\vert\,d_2\le d_1) = 6/21 \hs...
..._2=6\,\vert\,d_2\le d_1) = 1/21 \hspace{0.87 cm}[< P(d_2=6)]
\end{array}\right.$](img674.png)