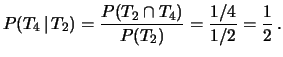Next: Condizionamento da eventi di
Up: Regole della probabilità
Previous: pzd100Dimostrazioni delle proprietà della
Indice
Relazione fra probabilità condizionata e
congiunta
Abbiamo già parlato del fatto che
l'evento condizionato
sia sostanzialmente lo stesso evento fisico del prodotto
logico con il
condizionante,
ma con una diversa condizione di incertezza in quanto subentra l'ipotesi che
il condizionante sia vero. La condizione aggiuntiva (rispetto all'ambiente
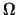 ) fa sì che in genere la probabilità di
) fa sì che in genere la probabilità di 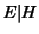 sia maggiore
di quella
di
sia maggiore
di quella
di 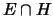 ogni qual volta che
ogni qual volta che
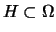 (``sottoinsieme
proprio'') e ovviamente
(``sottoinsieme
proprio'') e ovviamente
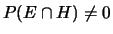 . In
effetti, ipotizzando che il ``fattore di amplificazione''
sia proprio
. In
effetti, ipotizzando che il ``fattore di amplificazione''
sia proprio 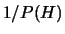 - se è diverso da zero -
si riottengono facilmente i casi limite di
- se è diverso da zero -
si riottengono facilmente i casi limite di  o
o
 .
In effetti in tutti i casi vale la relazione
.
In effetti in tutti i casi vale la relazione
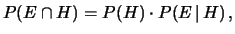 |
(4.16) |
da cui
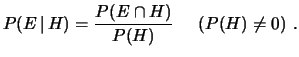 |
(4.17) |
Ovviamente i ruoli di  e di
e di 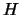 possono essere scambiati e
la (4.16)
può essere scritta più in generale
possono essere scambiati e
la (4.16)
può essere scritta più in generale
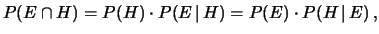 |
(4.18) |
Queste relazioni sono molto importanti per le applicazioni,
ma necessitano delle delucidazioni sul loro esatto significato,
al fine di capire quando è lecito utilizzarle.
Soprattutto può sorgere un po' di confusione in quanto a volte
si incontra la (4.17) indicata come
definizione della probabilità condizionata, altre volte
si incontra la (4.16) come teorema delle
probabilità composte. Vediamo come le formule appaiono nei diversi
approcci:
- nella valutazione combinatoria e frequentista la (4.16)
è una diretta consequenza della definizione.
Ad esempio,
se consideriamo la valutazione
combinatoria, indicando con
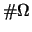 il
numero4.4 dei casi totali di
il
numero4.4 dei casi totali di
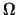 (la sua numerosità),
(la sua numerosità),
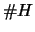 il numero di casi favorevoli ad
il numero di casi favorevoli ad 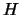 e
e
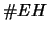 quelli favorevoli
a
quelli favorevoli
a  e
e 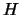 simultaneamente
si ottiene (ricordandosi della
(2.6)):
simultaneamente
si ottiene (ricordandosi della
(2.6)):
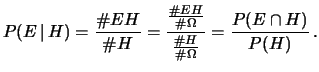 |
(4.19) |
Una analoga dimostrazione si ottiene per la valutazione delle
probabilità dalle frequenze relative.
- Anche nell'impostazione soggettivista la (4.16)
è un teorema, essendo essa condizione necessaria e sufficiente
per una scommessa coerente sull'evento
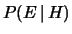 .
La dimostrazione è molto semplice. Si immagini di fare una
scommessa coerente
per vincere un importo unitario sull'evento condizionato
.
La dimostrazione è molto semplice. Si immagini di fare una
scommessa coerente
per vincere un importo unitario sull'evento condizionato 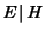 (vedi paragrafo 4.4):
si paga (con certezza!)
la cifra
(vedi paragrafo 4.4):
si paga (con certezza!)
la cifra
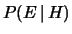 per vincere 1 se si verificano sia
per vincere 1 se si verificano sia  che
che 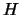 (con probabilità
(con probabilità
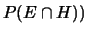 ;
nel caso che
;
nel caso che 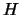 non si verifichi
(con probabilità
non si verifichi
(con probabilità
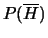 )
la scommessa viene invalidata e si recupera
la puntata
)
la scommessa viene invalidata e si recupera
la puntata
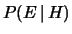 . Quindi la previsione di guadagno è:
. Quindi la previsione di guadagno è:
Essendo la scommessa coerente
e quindi nulla la previsione di guadagno, segue la
(4.16).
- Soltanto nell'approccio assiomatico la (4.17) è
presentata come definizione della probabilità condizionata
(anche se poi a volte la (4.18) viene chiamata
nello stesso testo ``teorema''...).
Ora se questa formula fosse veramente la definizione della probabilità
condizionata sarebbe necessario
valutare ogni volta
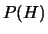 e
e
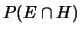 per poi ottenere
per poi ottenere
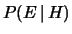 . Questo punto di vista è
chiaramente non accettabile e fortunatamente non è seguito
in pratica (nemmeno dalla maggior parte di
coloro che pensano che la
(4.17)
sia una definizione!).
. Questo punto di vista è
chiaramente non accettabile e fortunatamente non è seguito
in pratica (nemmeno dalla maggior parte di
coloro che pensano che la
(4.17)
sia una definizione!).
Si pensi a dei fisici che lavorano al progetto
di un nuovo rivelatore per la nuova generazione di acceleratori e
siano interessati
alla probabilità che un certo
algoritmo riesca a identificare un dato decadimento di
una nuova particella elementare,
ipotizzando una certa massa, certi modi di decadimento, dei parametri
del rivelatore, etc. Non è assolutamente pensabile valutare questa
probabilità condizionata dalla probabilità dei condizionanti
(che la particella esista sul serio, che abbia quella massa, etc)
e dalla congiunta dei condizionanti con l'evento ``il decadimento è
riconosciuto dall'algoritmo''). In pratica si fissano i valori
dei condizionanti nei programmi di simulazione e si valutano
le probabilità dalle frequenze.
Se questi esempi possono sembrare
un po' particolari, si provi a calcolare secondo la
(4.17) la probabilità che, avendo
estratto dalla tombola 40 numeri senza che sia uscito il ``47'',
questo esca al 41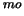 tentativo (la risposta ``al volo'' è 1/50).
tentativo (la risposta ``al volo'' è 1/50).
Nella maggior parte dei problemi pratici e scientifici è molto
più pratico (e in molti casi il solo metodo praticabile) assegnare
direttamente
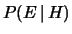 (ad
esempio come descritto nel paragrafo
2.6)
ed eventualmente da questa, se
(ad
esempio come descritto nel paragrafo
2.6)
ed eventualmente da questa, se 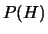 è diverso da zero,
calcolare
è diverso da zero,
calcolare
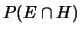 mediante la (4.16).
mediante la (4.16).
Facciamo un esempio banale ma che mostra a quali difficoltà si può
andare incontro prendendo
alla lettera la (4.17). Si consideri di lanciare
quattro volte una moneta regolare e di voler calcolare ``la probabilità
che al quarto lancio sia uscita Testa se anche
al secondo era uscita Testa". Chiaramente la risposta diretta di 1/2
è quella corretta. La si confronti con il seguente procedimento:
- -
- ci sono
 casi possibili, dei quali
casi possibili, dei quali
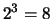 contengono Testa
al
contengono Testa
al 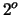 colpo e
colpo e 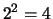 contengono Testa congiuntamente al
contengono Testa congiuntamente al 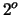 e al
e al 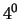 ;
;
- -
- quindi
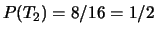 ,
,
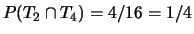 ,
da cui
,
da cui




Next: Condizionamento da eventi di
Up: Regole della probabilità
Previous: pzd100Dimostrazioni delle proprietà della
Indice
Giulio D'Agostini
2001-04-02
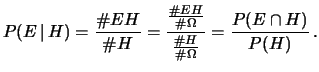
![]() tentativo (la risposta ``al volo'' è 1/50).
tentativo (la risposta ``al volo'' è 1/50).
![]() (ad
esempio come descritto nel paragrafo
2.6)
ed eventualmente da questa, se
(ad
esempio come descritto nel paragrafo
2.6)
ed eventualmente da questa, se ![]() è diverso da zero,
calcolare
è diverso da zero,
calcolare
![]() mediante la (4.16).
mediante la (4.16).