



Next: Distribuzione di probabilità e
Up: Variabili casuali e distribuzioni
Previous: Numeri aleatori
Indice
Se indichiamo con  (lettera maiuscola) la variabile e con
(lettera maiuscola) la variabile e con  i valori6.2
che può assumere,
associamo, all'evento
i valori6.2
che può assumere,
associamo, all'evento  la probabilità
la probabilità 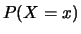 sulla base del nostro stato di conoscenza.
La variabile casuale
sulla base del nostro stato di conoscenza.
La variabile casuale  è detta discreta se
può assumere un numero finito (o una infinità
numerabile) di valori6.3.
Poiché
in molti problemi è possibile trovare delle funzioni
matematiche più o meno semplici con le quali descrivere le probabilità
di tutte le occorrenze di
è detta discreta se
può assumere un numero finito (o una infinità
numerabile) di valori6.3.
Poiché
in molti problemi è possibile trovare delle funzioni
matematiche più o meno semplici con le quali descrivere le probabilità
di tutte le occorrenze di  , è usuale
indicare6.4
tale probabilità con
, è usuale
indicare6.4
tale probabilità con 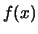 . In sintesi:
. In sintesi:
 indica la variabile casuale (esempio ``valore che verrà
indicato sul display della bilancia'');
indica la variabile casuale (esempio ``valore che verrà
indicato sul display della bilancia'');
 è il valore numerico che può assumere la variabile, con grado
di fiducia
è il valore numerico che può assumere la variabile, con grado
di fiducia 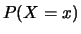 ;
;
-
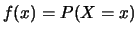 indica la funziona matematica mediante la quale
assegnamo la probabilità di tutti i possibili valori
indica la funziona matematica mediante la quale
assegnamo la probabilità di tutti i possibili valori  di
di  .
.
- quando sono specificati i valori
 che la variabile
che la variabile  può assumere,
insieme alla funzione di probabilità
può assumere,
insieme alla funzione di probabilità 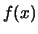 , si parla
di distribuzione di probabilità.
, si parla
di distribuzione di probabilità.
Figura:
Costruzione di una variabile casuale.
 |
Nel seguito vedremo alcune distribuzioni di probabilità.
Anche se talvolta si arriverà a formule che possono sembrare
complicate, bisogna tenere conto che lo schema di valutazione
della probabilità è lo stesso presentato nei capitoli
precedenti:
- in base allo stato di conoscenze si assegna un certo valore
di probabilità a eventi elementari;
- usando le regole della probabilità si calcolano le probabilità
di eventi più complicati ottenuti da operazioni logiche sui primi;
- la sola condizione importante per la costruzione della variabile
casuale è che ad ogni evento considerato sia associata sempre
e univocamente
(ma non necessariamente biunivocamente)
una variabile numerica, come mostrato in figura 6.1.
Questo sta ad indicare che l'insieme degli eventi
``
 assume il valore
assume il valore  '' costituisce, quando
si considerano
tutti i possibili valori di
'' costituisce, quando
si considerano
tutti i possibili valori di  , una classe completa.
, una classe completa.
Gli esempi dei prossimi paragrafi dovrebbero
chiarire gli eventuali dubbi.




Next: Distribuzione di probabilità e
Up: Variabili casuali e distribuzioni
Previous: Numeri aleatori
Indice
Giulio D'Agostini
2001-04-02