${\bf\circlearrowright }$ Distribuzione di probabilità e distribuzioni statistiche

Prima di intraprendere lo studio sistematico delle distribuzioni di probabilità, è opportuno chiarire la differenza fra queste distribuzioni e le distribuzioni statistiche. Esse sono infatti legate da molti aspetti comuni, come una analoga terminologia per gli indicatori di centralità e di dispersione (concetti che saranno introdotti nei paragrafi 6.8, 6.9 e 6.11) e analoghe rappresentazioni grafiche.

Per chiarire meglio cosa si intende con i due tipi di distribuzioni, è opportuno fare un accenno alla differenza fra statistica descrittiva e statistica inferenziale. Infatti il termine stesso statistica viene usato in vari contesti e a volte, non del tutto propriamente, anche come sinonimo di probabilità.

Senza voler entrare nei dettagli, diciamo che bisogna distinguere le statistiche, di cui si parla in continuazione, dalla statistica. Le ``statistiche'' stanno ad indicare sintesi di dati su aspetti sociali, economici, politici, geografici, e così via (``le statistiche dicono'' che ``il ...% della popolazione è ultrasessantenne'', che ``questa è l'estate più calda degli ultimi $n$ anni'', che ``il ...% delle coppie divorzia nei primi 5 anni di matrimonio'', etc.).

Con statistica si intende invece la disciplica che, in senso lato, si interessa della raccolta e l'analisi dei dati e dell'interpretazione dei risultati. In particolare, la statistica descrittiva si occupa di descrivere la massa dei dati sperimentali con pochi numeri o grafici significativi. Quindi, per così dire si occupa di fotografare una data situazione e di sintetizzarne le caratteristiche salienti. La statistica inferenziale utilizza i dati statistici, generalmente sintetizzati dalla statistica descrittiva, per fare previsioni di tipo probabilistico su situazioni future o comunque incerte. Ad esempio esaminando un piccolo campione estratto da una grande popolazione si può cercare di valutare la frazione della popolazione che possiede una certa caratteristica, ha un certo reddito, voterà per un certo candidato.

Per quello che riguarda la teoria e la pratica delle misure, indubbiamente quella più interessante è la statistica inferenziale in quanto scopo delle misure è quello di fare affermazioni sul valore di una grandezza o sulla validità di una teoria a partire da un numero limitato di misure, effettuate con strumenti non ideali, con parametri e disturbi ambientali della cui entità non si è assolutamente certi.

Anche la statistica descrittiva ha una sua importanza, in quanto nella maggior parte dei casi non è necessario conoscere il dettaglio di tutti i dati sperimentali raccolti per inferire qualcosa, ma spesso sono sufficienti pochi numeri nei quali i dati sono stati precedentemente sintetizzati. Quindi, lo schema di massima che si usa nella statistica inferenziale è formato dai seguenti passi:

1. raccolta dei dati sperimentali;
2. sintesi statistiche (statistica descrittiva);
3. inferenza (affermazioni probabilistiche);

Come si può immaginare, questa classificazione è artificiosa ed è difficile separare i tre stadi. Ad esempio, è difficile raccogliere dati statistici su un campione della popolazione se non si ha nessuna idea della caratteristiche della popolazione stessa (si pensi agli ``exit poll''), oppure fare delle misure i cui risultati siano utilizzabili se non si conosce la fenomenologia sulla quale si sta indagando con tutti gli effetti sistematici. Infatti, il primo punto racchiude tutta l'arte della sperimentazione, a partire dalla conoscenza della fenomenologia e degli strumenti, alla progettazione, realizzazione e conduzione dell'esperimento. Così pure, alcune grandezza di sintesi di dati statistici sono costruite già pensando ad un successivo uso inferenziale (si pensi alla deviazione standard di una distribuzione statistica calcolata dividendo la somma dei quadrati degli scarti per 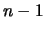$n-1$ invece di $n$). Tornando alle distribuzioni, possiamo dire che la differenza sostanziale fra i due tipi è che, mentre le distribuzioni di probabilità, fanno riferimento a variabili casuali, ovvero a numeri rispetto ai quali siamo in stato di incertezza, le distribuzioni statistiche descrivono variabili statistiche, ovvero occorrenze certe nel passato di determinati valori (o classi di valori). In sintesi:

• le distribuzioni di probabilità associano ad ogni valore una funzione che esprime il grado di fiducia sul suo realizzarsi
• le distribuzioni statistiche associano ad ogni valore (o classe di valori) un peso statistico pari alla frequenza relativa con cui esso si è verificato nel passato.

Ovviamente, come le frequenze di eventi giocano un ruolo importante nella valutazione della probabilità, così le distribuzioni statistiche hanno una analoga importanza nella valutazione delle distribuzioni di probabilità, anche se, come vedremo (già a partire dal paragrafo 7.15), a nessuna persona ragionevole dovrebbe venire in mente di affermare che la distribuzione di probabilità è data esattamente dalla distribuzione statistica osservata.

Altri commenti su differenze e analogie fra i due tipi di distribuzione verranno fatti nel paragrafo 6.18.