


Next: Sources of asymmetric uncertainties
Up: Asymmetric Uncertainties: Sources, Treatment
Previous: Introduction
Propagating uncertainty
Determining the value of a physics quantity is seldom
an end in itself.
In most cases the result is used, together with other
experimental and theoretical quantities, to
calculate the value of other quantities of interest.
As it is well understood, uncertainty on the value of each
ingredient is propagated into uncertainty on the
final result.
If uncertainty is quantified by probability, as it is commonly done
explicitly or implicitly2 in physics, the propagation
of uncertainty is performed using rules based on probability theory.
If we indicate by
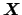 the set
(`vector') of input quantities and by
the set
(`vector') of input quantities and by 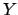 the
final quantity, given by the function
the
final quantity, given by the function
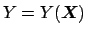 of the
input quantities, the most general propagation formula
(see e.g. [3])
is given by (we stick to continuous variables):
of the
input quantities, the most general propagation formula
(see e.g. [3])
is given by (we stick to continuous variables):
![\begin{displaymath}
f(y) = \int\! \delta[y-Y({\mbox{\boldmath$x$}})]\cdot f({\mbox{\boldmath$x$}}) \mbox{d}{\mbox{\boldmath$x$}} ,
\end{displaymath}](img14.png) |
(1) |
where 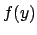 is the p.d.f. of
is the p.d.f. of 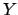 ,
,
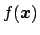 stands for the joint p.d.f. of
stands for the joint p.d.f. of
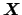 and
and 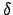 is the Dirac delta
(note the use of capital letters to name variables and small
letters to indicate the values that variables may assume).
The exact evaluation of Eq. (1) is often challenging,
but, as discussed in Ref. [3], this formula has a
nice simple interpretation
that makes its Monte Carlo implementation conceptually easy.
is the Dirac delta
(note the use of capital letters to name variables and small
letters to indicate the values that variables may assume).
The exact evaluation of Eq. (1) is often challenging,
but, as discussed in Ref. [3], this formula has a
nice simple interpretation
that makes its Monte Carlo implementation conceptually easy.
As it is also well known, often there is no need to go through the
analytic, numerical or Monte Carlo evaluation of Eq.(1),
since linearization of
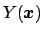 around the expected value
of
around the expected value
of
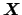 (E[
(E[
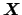 ]) makes the calculation of
expected value and variance of
]) makes the calculation of
expected value and variance of 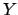 very easy, using the well known
standard propagation formulae, that for uncorrelated input quantities are
very easy, using the well known
standard propagation formulae, that for uncorrelated input quantities are
As far as the shape of 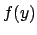 , a Gaussian one is usually assumed,
as a result of the central limit theorem.
Holding this assumptions,
, a Gaussian one is usually assumed,
as a result of the central limit theorem.
Holding this assumptions,
![$\mbox{E}[Y]$](img24.png) and
and 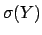 is all what we need.
is all what we need.
![$\mbox{E}[Y]$](img24.png) gives the `best value', and
probability intervals, upper/lower limits and so on
can be easily calculated.
In particular, within the Gaussian approximation,
the most believable value (mode), the barycenter of the
p.d.f. (expected value) and the value that separates
two adjacent 50% probability intervals (median) coincide.
If
gives the `best value', and
probability intervals, upper/lower limits and so on
can be easily calculated.
In particular, within the Gaussian approximation,
the most believable value (mode), the barycenter of the
p.d.f. (expected value) and the value that separates
two adjacent 50% probability intervals (median) coincide.
If 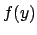 is asymmetric this is not any longer true and one
needs then to clarify what `best value' means,
which could be one of the above three position parameters,
or something else (in the Bayesian approach
`best value' stands for expected value, unless differently specified).
is asymmetric this is not any longer true and one
needs then to clarify what `best value' means,
which could be one of the above three position parameters,
or something else (in the Bayesian approach
`best value' stands for expected value, unless differently specified).
Anyhow, Gaussian approximation is not the main issue here and, in most
real applications, characterized by several contributions to the
combined uncertainty about 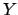 ,
this approximation is a reasonable one, even when some of the input
quantities individually contribute asymmetrically.
My concerns in this paper are more related to the evaluation
of
,
this approximation is a reasonable one, even when some of the input
quantities individually contribute asymmetrically.
My concerns in this paper are more related to the evaluation
of ![$\mbox{E}[Y]$](img24.png) and
and 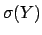 when
when
- instead of
Eqs. (2)-(3),
ad hoc
propagation prescriptions are used
in presence of asymmetric uncertainties;
- linearization implicit in
Eqs. (2)-(3)
is not a good approximation.
Let us start with the first point, considering, as
an easy academic example, input quantities described by the
asymmetric triangular distribution
shown in the left plot of Fig. 1.
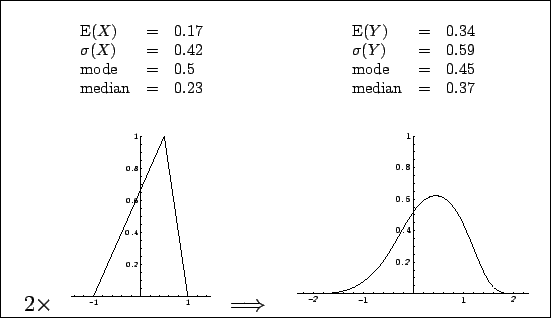
Figure:
Distribution of the
sum of two independent quantities, each described by an asymmetric
triangular p.d.f. self-defined in the left plot.
The resulting p.d.f.
(right plot) has been calculated analytically making use of
Eq.(1).
This figure corresponds to Fig. 4.3 of Ref. [3].
 |
The value of 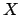 can range between
can range between 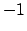 and
and 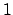 , with a
`best value', in the sense of maximum probability value,
of 0.5. The interval
, with a
`best value', in the sense of maximum probability value,
of 0.5. The interval
![$[-0.16, +0.72]$](img30.png) gives a 68.3% probability
interval, and the `result' could be reported
as
gives a 68.3% probability
interval, and the `result' could be reported
as
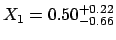 . This is not a problem as long as we known
what this notation means and, possibly, know the shape of
. This is not a problem as long as we known
what this notation means and, possibly, know the shape of 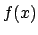 .
The problem arises when we want
to make use of this result and we do not have access to
.
The problem arises when we want
to make use of this result and we do not have access to
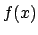 (as it is often the case), or we make improper use
of the information [i.e. in the case we are aware of
(as it is often the case), or we make improper use
of the information [i.e. in the case we are aware of 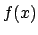 ].
Let us assume, for simplicity,
to have a second independent quantity,
].
Let us assume, for simplicity,
to have a second independent quantity, 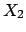 , described exactly by
the same p.d.f. and reported in the same way:
, described exactly by
the same p.d.f. and reported in the same way:
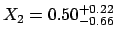 . Imagine we are now interested
to the quantity
. Imagine we are now interested
to the quantity 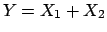 . How to report the result about
. How to report the result about 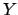 , based
on the results about
, based
on the results about 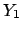 and
and 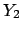 ? Here are some common,
but wrong ways to give the result:
? Here are some common,
but wrong ways to give the result:
- asymmetric uncertainties added in quadrature:
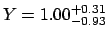 ;
;
- asymmetric uncertainties added linearly:
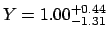 .
.
Indeed, in this simple case we can calculate
the integral (1)
analytically, obtaining the curve shown in the
plot on the right side of
Fig. 1, where several position and
shape parameters have also been reported. The `best value' of 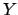 ,
meant as expected value (i.e. the barycenter of the p.d.f.)
comes out to be 0.34. Even those who like to think at the
`best value' as the value of maximum probability (density)
would choose 0.45 (note that in this particular example the mode of the sum
is smaller than the mode of each addend!). Instead,
a `best value' of
,
meant as expected value (i.e. the barycenter of the p.d.f.)
comes out to be 0.34. Even those who like to think at the
`best value' as the value of maximum probability (density)
would choose 0.45 (note that in this particular example the mode of the sum
is smaller than the mode of each addend!). Instead,
a `best value' of 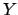 of 1.00 obtained by the ad hoc
rules, unfortunately often used in physics, corresponds neither
to mode, nor to expected value or median.
of 1.00 obtained by the ad hoc
rules, unfortunately often used in physics, corresponds neither
to mode, nor to expected value or median.
The situation would have been much better if
expected value and standard deviation of 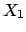 and
and 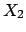 had been reported (respectively 0.17 and 0.42). Indeed, these
are the quantities that
matter in `error propagation', because the theorems upon which
propagation formulae rely -- exactly in the case
had been reported (respectively 0.17 and 0.42). Indeed, these
are the quantities that
matter in `error propagation', because the theorems upon which
propagation formulae rely -- exactly in the case 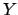 is a linear combination
of
is a linear combination
of
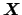 , or approximately in the case linearization has been performed --
speak of expected values and variances.
It is easy to verify from the numbers in Fig. 1
that exactly the correct values of
, or approximately in the case linearization has been performed --
speak of expected values and variances.
It is easy to verify from the numbers in Fig. 1
that exactly the correct values of
![$\mbox{E}[Y] = 0.34$](img41.png) and
and
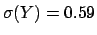 would have been obtained.
Moreover, one can see that
expected value, mode and median of
would have been obtained.
Moreover, one can see that
expected value, mode and median of 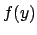 do not differ much from
each other, and the shape of
do not differ much from
each other, and the shape of 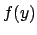 resembles a somewhat
skewed Gaussian. When
resembles a somewhat
skewed Gaussian. When 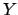 will be combined with other quantities
in a next analysis its slightly non-Gaussian shape
will not matter any longer. Note that we have achieved this nice
result already with only two input quantities. If we had a few
more,
already
will be combined with other quantities
in a next analysis its slightly non-Gaussian shape
will not matter any longer. Note that we have achieved this nice
result already with only two input quantities. If we had a few
more,
already 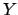 would have been much Gaussian-like. Instead,
performing a bad combination of several quantities all skewed in the
same side would yield `divergent'
results3:
for
would have been much Gaussian-like. Instead,
performing a bad combination of several quantities all skewed in the
same side would yield `divergent'
results3:
for 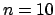 we get,
using a quadratic combination of left and right deviations,
we get,
using a quadratic combination of left and right deviations,
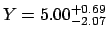 versus the correct
versus the correct
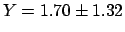 .
.
As conclusion from this section I would like to make some points:
- in case of asymmetric uncertainty on a quantity,
it should be avoided to report only
most probable value and a probability interval
(be it 68.3%, 95%, or what else);
- expected value, meant as barycenter of the distribution,
as well as standard deviations should always be reported,
providing also the shape of the distribution (or its summary
in terms of shape parameters, or even a parameterization of the
log-likelihood function in a
polynomial form, as done e.g. in Ref. [9]),
if the distribution is asymmetric or non trivial.
Note that the propagation example shown here is the most
elementary possible. The situation gets more complicate if
also nonlinear propagation is involved (see Sec. 3.2)
or when quantities are used in fits (see e.g. Sec. 12.1 of
Ref. [3]).
Hoping that the reader is, at this point, at least
worried about the effects of badly treated asymmetric uncertainties,
let us now review
the sources of asymmetric uncertainties.



Next: Sources of asymmetric uncertainties
Up: Asymmetric Uncertainties: Sources, Treatment
Previous: Introduction
Giulio D'Agostini
2004-04-27
![]() the set
(`vector') of input quantities and by
the set
(`vector') of input quantities and by ![]() the
final quantity, given by the function
the
final quantity, given by the function
![]() of the
input quantities, the most general propagation formula
(see e.g. [3])
is given by (we stick to continuous variables):
of the
input quantities, the most general propagation formula
(see e.g. [3])
is given by (we stick to continuous variables):
![]() around the expected value
of
around the expected value
of
![]() (E[
(E[
![]() ]) makes the calculation of
expected value and variance of
]) makes the calculation of
expected value and variance of ![]() very easy, using the well known
standard propagation formulae, that for uncorrelated input quantities are
very easy, using the well known
standard propagation formulae, that for uncorrelated input quantities are
![]() ,
this approximation is a reasonable one, even when some of the input
quantities individually contribute asymmetrically.
My concerns in this paper are more related to the evaluation
of
,
this approximation is a reasonable one, even when some of the input
quantities individually contribute asymmetrically.
My concerns in this paper are more related to the evaluation
of ![]() and
and ![]() when
when

![]() and
and ![]() had been reported (respectively 0.17 and 0.42). Indeed, these
are the quantities that
matter in `error propagation', because the theorems upon which
propagation formulae rely -- exactly in the case
had been reported (respectively 0.17 and 0.42). Indeed, these
are the quantities that
matter in `error propagation', because the theorems upon which
propagation formulae rely -- exactly in the case ![]() is a linear combination
of
is a linear combination
of
![]() , or approximately in the case linearization has been performed --
speak of expected values and variances.
It is easy to verify from the numbers in Fig. 1
that exactly the correct values of
, or approximately in the case linearization has been performed --
speak of expected values and variances.
It is easy to verify from the numbers in Fig. 1
that exactly the correct values of
![]() and
and
![]() would have been obtained.
Moreover, one can see that
expected value, mode and median of
would have been obtained.
Moreover, one can see that
expected value, mode and median of ![]() do not differ much from
each other, and the shape of
do not differ much from
each other, and the shape of ![]() resembles a somewhat
skewed Gaussian. When
resembles a somewhat
skewed Gaussian. When ![]() will be combined with other quantities
in a next analysis its slightly non-Gaussian shape
will not matter any longer. Note that we have achieved this nice
result already with only two input quantities. If we had a few
more,
already
will be combined with other quantities
in a next analysis its slightly non-Gaussian shape
will not matter any longer. Note that we have achieved this nice
result already with only two input quantities. If we had a few
more,
already ![]() would have been much Gaussian-like. Instead,
performing a bad combination of several quantities all skewed in the
same side would yield `divergent'
results3:
for
would have been much Gaussian-like. Instead,
performing a bad combination of several quantities all skewed in the
same side would yield `divergent'
results3:
for ![]() we get,
using a quadratic combination of left and right deviations,
we get,
using a quadratic combination of left and right deviations,
![]() versus the correct
versus the correct
![]() .
.