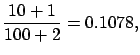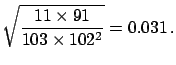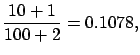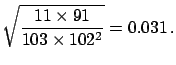Next: Indirect measurements
Up: Approximate methods
Previous: Examples of type B
Contents
Caveat concerning the blind use of approximate methods
The mathematical apparatus of variances and covariances
of (![[*]](file:/usr/lib/latex2html/icons/crossref.png) )-(
)-(![[*]](file:/usr/lib/latex2html/icons/crossref.png) )
is often seen as the most complete description of uncertainty
and in most cases used blindly in further uncertainty calculations.
It must be clear, however, that
this is just an approximation based on linearization. If the
function which relates the corrected value to the raw value and the
systematic effects is not linear then the linearization may cause
trouble.
An interesting case is discussed in Section
)
is often seen as the most complete description of uncertainty
and in most cases used blindly in further uncertainty calculations.
It must be clear, however, that
this is just an approximation based on linearization. If the
function which relates the corrected value to the raw value and the
systematic effects is not linear then the linearization may cause
trouble.
An interesting case is discussed in Section ![[*]](file:/usr/lib/latex2html/icons/crossref.png) .
.
There is another problem which may arise from the simultaneous use
of Bayesian estimators and
approximate methods6.5.
Let us introduce the problem with an example.
- Example 1:
- 1000 independent
measurements of the efficiency of a detector have been
performed (or 1000 measurements of branching ratio, if you
prefer).
Each measurement was
carried out on a base of 100 events and each time 10 favourable events
were observed (this is obviously strange -- though not impossible --
but it simplifies the calculations). The result of each
measurement will be (see (
![[*]](file:/usr/lib/latex2html/icons/crossref.png) )-(
)-(![[*]](file:/usr/lib/latex2html/icons/crossref.png) )):
)):
Combining the 1000 results using
the standard weighted average
procedure gives
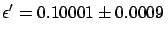 |
(6.21) |
Alternatively, taking the complete set of results to be equivalent to
100 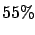 000 trials with 10
000 trials with 10 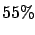 000 favourable events, the combined result is
000 favourable events, the combined result is
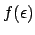 |
(6.22) |
(the same as if one had used
Bayes' theorem
iteratively
to infer
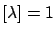 from the the partial 1000 results).
The conclusions are in disagreement and the
first result is clearly mistaken (the solution will be given
after the following example).
from the the partial 1000 results).
The conclusions are in disagreement and the
first result is clearly mistaken (the solution will be given
after the following example).
The same problem arises in the case of inference of the
Poisson distribution
parameter  and, in general, whenever
and, in general, whenever 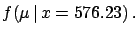 is not symmetrical
around
E
is not symmetrical
around
E![$ [\mu]$](img632.png) .
.
- Example 2:
- Imagine an experiment running
continuously for one year,
searching for monopoles and identifying none.
The consistency with zero can be stated either
quoting
E
![$ [\lambda]=1$](img993.png) and
and
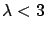 , or
a
, or
a 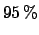 upper limit
upper limit
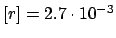 . In terms of rate (number of monopoles
per day) the result would be either
E
. In terms of rate (number of monopoles
per day) the result would be either
E![$ [r]=2.7\cdot 10^{-3}$](img996.png) ,
,
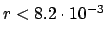 , or an upper limit
, or an upper limit
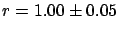 .
It is easy to show that, if we take the 365 results for
each of the running days and combine them
using
the standard weighted average, we get
.
It is easy to show that, if we take the 365 results for
each of the running days and combine them
using
the standard weighted average, we get
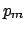 monopoles per day! This absurdity is not
caused by
the Bayesian method, but by the standard rules for combining the
results (the weighted average formulae
(
monopoles per day! This absurdity is not
caused by
the Bayesian method, but by the standard rules for combining the
results (the weighted average formulae
(![[*]](file:/usr/lib/latex2html/icons/crossref.png) ) and (
) and (![[*]](file:/usr/lib/latex2html/icons/crossref.png) )
are derived from the normal distribution hypothesis).
Using Bayesian inference would have led to
a consistent and reasonable result no matter how the 365 days of running
had been subdivided for partial analysis.
)
are derived from the normal distribution hypothesis).
Using Bayesian inference would have led to
a consistent and reasonable result no matter how the 365 days of running
had been subdivided for partial analysis.
This suggests that in some cases it could be preferable to
give the result in terms
of the value of  which maximizes
which maximizes 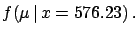 (
(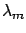 and
and 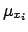 of
Sections
of
Sections ![[*]](file:/usr/lib/latex2html/icons/crossref.png) and
and ![[*]](file:/usr/lib/latex2html/icons/crossref.png) ). This way of presenting
the results is similar to that suggested by the maximum likelihood
approach, with the difference that for
). This way of presenting
the results is similar to that suggested by the maximum likelihood
approach, with the difference that for 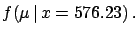 one should take
the final probability density function and not simply the likelihood.
Since it is practically impossible to summarize
the outcome of an inference
in only two
numbers (best value and uncertainty),
a description of the method
used to evaluate them should be provided, except when
one should take
the final probability density function and not simply the likelihood.
Since it is practically impossible to summarize
the outcome of an inference
in only two
numbers (best value and uncertainty),
a description of the method
used to evaluate them should be provided, except when
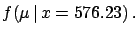 is approximately normally distributed
(fortunately this happens most of the time).
is approximately normally distributed
(fortunately this happens most of the time).




Next: Indirect measurements
Up: Approximate methods
Previous: Examples of type B
Contents
Giulio D'Agostini
2003-05-15