Keeping the notation 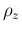 for the ratio of the generic
Gamma distributed variables
for the ratio of the generic
Gamma distributed variables 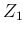 and
and 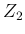 , the pdf
of Eq. (
, the pdf
of Eq. (![[*]](crossref.png) ) can be further
simplified reminding that the beta
special function (or Euler integral of the
first kind [33]), defined as
) can be further
simplified reminding that the beta
special function (or Euler integral of the
first kind [33]), defined as
can be written as
We can then rewrite the combination of three gamma
functions appearing in Eq. (![[*]](crossref.png) )
as
)
as
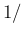 B
B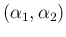 ,
thus getting
,
thus getting
As far as mode, expected value and variance are concerned,
they can be obtained, without direct calculations,
just transforming those of
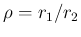 , seen above,
remembering that, starting from a flat prior,
, seen above,
remembering that, starting from a flat prior,
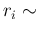 Gamma
Gamma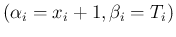 .
We get then
.
We get then
mode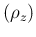 |
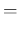 |
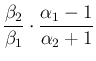 |
(73) |
| |
|
|
|
E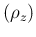 |
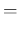 |
 |
(74) |
| |
|
|
|
Var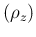 |
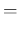 |
![$\displaystyle \frac{\beta_2^2}{\beta_1^2}\cdot
\left[ \frac{\alpha_1}{\alpha_2-...
...\frac{\alpha_1}{\alpha_2-1}\right)\right]
\hspace{0.85cm}(\mathbf{\alpha_2>2}).$](img351.png) |
(75) |
Moreover, just for completeness, let us mention
the special case
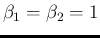 , that
written for the generic variable
, that
written for the generic variable 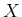 , becomes
, becomes
`known' (certainly not to me before I was
attempting to write these subsection)
as Beta prime distribution [34],
with parameters 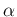 and
and 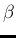 :
:
The name of the distribution is clearly due to the special function
resulting from normalization. It is `prime'
in order to distinguish it
from the more famous (and more important as far as
practical applications are concerned)
Beta distribution which arises quite `naturally' when inferring
the parameter 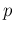 of the Bernoulli trials, in the light of
of the Bernoulli trials, in the light of
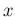 successes in
successes in 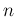 trials (essentially the original problem
tackled by Bayes [19] and Laplace [20]),
and then used as conjugate
prior of the binomial distribution
(see e.g. Ref. [30] as well as
Ref. [1] for practical applications).
The Beta prime distribution
is actually what has been independently derived in
Sec.
trials (essentially the original problem
tackled by Bayes [19] and Laplace [20]),
and then used as conjugate
prior of the binomial distribution
(see e.g. Ref. [30] as well as
Ref. [1] for practical applications).
The Beta prime distribution
is actually what has been independently derived in
Sec. ![[*]](crossref.png) to describe
to describe
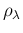 , although
the beta special function was not used there,
nor in Sec.
, although
the beta special function was not used there,
nor in Sec. ![[*]](crossref.png) .
.
![[*]](crossref.png) ) can be further
simplified reminding that the beta
special function (or Euler integral of the
first kind [33]), defined as
) can be further
simplified reminding that the beta
special function (or Euler integral of the
first kind [33]), defined as
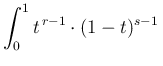 d
d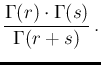
![[*]](crossref.png) )
as
)
as
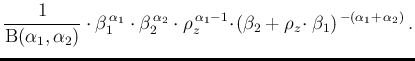
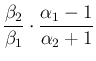

![$\displaystyle \frac{\beta_2^2}{\beta_1^2}\cdot
\left[ \frac{\alpha_1}{\alpha_2-...
...\frac{\alpha_1}{\alpha_2-1}\right)\right]
\hspace{0.85cm}(\mathbf{\alpha_2>2}).$](img351.png)
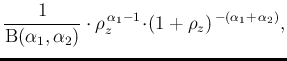
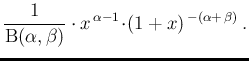
![[*]](crossref.png) to describe
to describe
![[*]](crossref.png) .
.