Next: Inferred distribution of Up: Ratio of counts vs Previous: More on the ratio
![[*]](crossref.png) . But this is not the only way to approach
the problem.
An alternative model is shown in Fig.
. But this is not the only way to approach
the problem.
An alternative model is shown in Fig. ![[*]](crossref.png) ,
in which the node
,
in which the node
Writing one diagram or another one is not just a question
of drawing art. Indeed, the network reflects the supposed causal model
(`what depends from what') and therefore
the choice of the model can have an effect on the results.
It is therefore important to understand in what they differ.
In the model of Fig. ![[*]](crossref.png) the rates
the rates ![]() and
and ![]() assume a primary role. We infer their values and,
as a byproduct, we get
assume a primary role. We infer their values and,
as a byproduct, we get ![]() . In this new model, instead,
it is
. In this new model, instead,
it is ![]() to have a primary role, together with one of the
two rates (they cannot be both at the same level because
there is a constraint between the three quantities).
Our choice to make
to have a primary role, together with one of the
two rates (they cannot be both at the same level because
there is a constraint between the three quantities).
Our choice to make ![]() depend on
depend on ![]() is due to the fact
that
is due to the fact
that ![]() , appearing at the denominator,
can be seen as a
`baseline' to which the other rate is referred
(obviously, here
, appearing at the denominator,
can be seen as a
`baseline' to which the other rate is referred
(obviously, here ![]() and
and ![]() are just names, and
therefore the choice of their role depend on their meaning).
are just names, and
therefore the choice of their role depend on their meaning).
The strategy to get
![]() is then different, being
this time
is then different, being
this time ![]() directly inferred using the Bayes theorem applied to the
entire network.
A strong advantage of this second model
is that, as we shall see, its prior can be factorized
(see also Ref. [1], especially
Appendix A there, in which there is a summary
of the formulae we are going to use).
directly inferred using the Bayes theorem applied to the
entire network.
A strong advantage of this second model
is that, as we shall see, its prior can be factorized
(see also Ref. [1], especially
Appendix A there, in which there is a summary
of the formulae we are going to use).
In analogy to what has been done
in detail in Ref. [1], the pdf of ![]() is obtained in two steps: first infer
is obtained in two steps: first infer
![]() ;
then get the pdf of
;
then get the pdf of ![]() by marginalization.
For the first step we need to write down the joint distribution of all
variables in the network (apart from
by marginalization.
For the first step we need to write down the joint distribution of all
variables in the network (apart from ![]() and
and ![]() which we consider
just as fixed parameters, having usually negligible uncertainty)
using the most convenient chain rule,
obtained navigating bottom up the graphical model.
Indicating, as in Ref. [1], with
which we consider
just as fixed parameters, having usually negligible uncertainty)
using the most convenient chain rule,
obtained navigating bottom up the graphical model.
Indicating, as in Ref. [1], with ![]() the joint pdf
of all relevant variables, we obtain from the chain rule
the joint pdf
of all relevant variables, we obtain from the chain rule
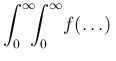 d d |
(79) | ||
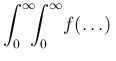 d d |
(80) |