For completeness, let us also try to get the closed expressions
of
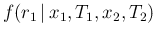 and
and
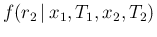 , although only under the assumption
of a flat prior of
, although only under the assumption
of a flat prior of 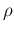 . In this case this choice is forced
from the fact that
. In this case this choice is forced
from the fact that
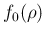 cannot be expressed in term of a conjugate prior
which would then simplify the calculations. For the general case, in fact,
we have to change methods, moving to Markov Chain
Monte Carlo (MCMC), as done e.g.
in Ref. [1] and as it will be sketched in the next section.
cannot be expressed in term of a conjugate prior
which would then simplify the calculations. For the general case, in fact,
we have to change methods, moving to Markov Chain
Monte Carlo (MCMC), as done e.g.
in Ref. [1] and as it will be sketched in the next section.
In order to get the pdf of 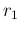 , we need to restart from
the unnormalized joint distribution (
, we need to restart from
the unnormalized joint distribution (![[*]](crossref.png) ),
proceeding then like in Eq. (
),
proceeding then like in Eq. (![[*]](crossref.png) ),
but this time integrating over
),
but this time integrating over 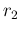 and
and 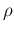 and absorbing the constant priors in the proportionality factor:
and absorbing the constant priors in the proportionality factor:
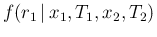 |
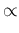 |
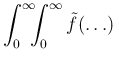 d d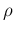 d d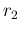 |
(108) |
| |
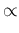 |
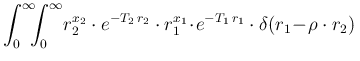 d d d d |
(109) |
| |
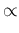 |
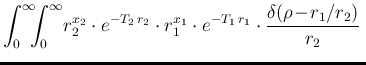 d d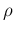 d d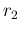 |
(110) |
| |
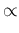 |
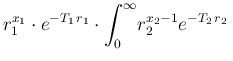 d d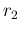 |
(111) |
| |
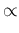 |
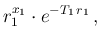 |
(112) |
thus reobtaining, besides normalization,
Eq. (![[*]](crossref.png) ).
).
Similarly, we have
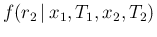 |
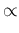 |
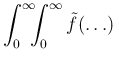 d d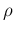 d d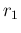 |
(113) |
| |
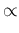 |
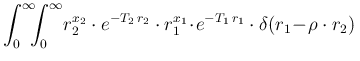 d d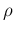 d d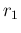 |
(114) |
| |
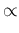 |
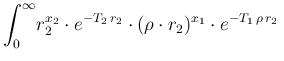 d d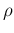 |
(115) |
| |
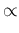 |
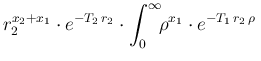 d d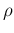 |
(116) |
| |
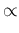 |
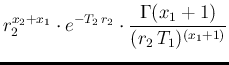 |
(117) |
| |
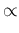 |
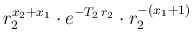 |
(118) |
| |
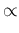 |
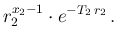 |
(119) |
We see that, differently from
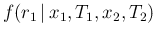 ,
the power of
,
the power of 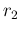 is, instead of
is, instead of 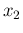 ,
, 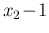 ,
that is we get an effect similar to that found for the
distribution of
,
that is we get an effect similar to that found for the
distribution of 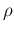 . As a consequence, expected values
and standard deviation of
. As a consequence, expected values
and standard deviation of 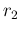 are
are 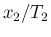 and
and
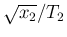 , respectively.
, respectively.
![]() , we need to restart from
the unnormalized joint distribution (
, we need to restart from
the unnormalized joint distribution (![[*]](crossref.png) ),
proceeding then like in Eq. (
),
proceeding then like in Eq. (![[*]](crossref.png) ),
but this time integrating over
),
but this time integrating over ![]() and
and ![]() and absorbing the constant priors in the proportionality factor:
and absorbing the constant priors in the proportionality factor:
![[*]](crossref.png) ).
).