Use of MCMC methods to cross-check the closed results
and to analyze extended models
So far our models have been rather simple,
missing however several real life complications. For example,
assuming that we do observe the number of counts
due to a Poisson distribution with a given
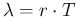 clearly implies that we are neglecting efficiency issues.
In order to include efficiencies
we need to modify our graphical model of
Fig.
clearly implies that we are neglecting efficiency issues.
In order to include efficiencies
we need to modify our graphical model of
Fig. ![[*]](crossref.png) (hereafter we stick to this last model),
adding the relevant nodes.
(hereafter we stick to this last model),
adding the relevant nodes.
The extended model is shown in Fig. ![[*]](crossref.png) ,
,
Figure:
Extension of the model of Fig. ![[*]](crossref.png) in order to include efficiencies.
in order to include efficiencies.
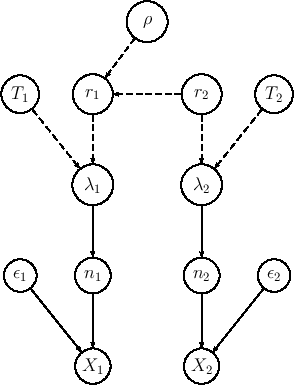 |
in which we have redefined the symbols, keeping 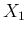 and
and 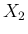 associated
to the observed counts and then calling
associated
to the observed counts and then calling 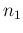 and
and 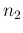 those
`produced' by the Poissonians. Each
those
`produced' by the Poissonians. Each 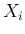 is then binomially
distributed with parameters
is then binomially
distributed with parameters 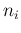 and
and
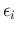 . In summary,
listing the `causal relations' from bottom to top, we have
. In summary,
listing the `causal relations' from bottom to top, we have
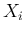 |
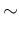 |
Binom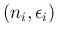 |
(120) |
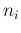 |
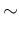 |
Poisson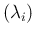 |
(121) |
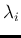 |
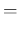 |
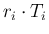 |
(122) |
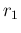 |
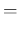 |
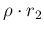 |
(123) |
At this point we can easily build up the joint distribution
of all quantities in the network, as we have done in the previous section,
and then evaluate the (possibly joint) distribution of the
variables of interest, conditioned by those which are observed
or somehow assumed. Moreover, also the efficiencies
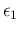 and
and
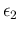 are by themselves uncertain, and then
we have to integrate also over them, taking into account
their probability distributions
are by themselves uncertain, and then
we have to integrate also over them, taking into account
their probability distributions
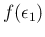 and
and
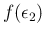 .
In fact, their value come from test experiments or, more likely,
from Monte Carlo simulations of the physics process and of the
detector. So we need to enlarge
the model adding four other nodes, taking into account
the probabilistic links
.
In fact, their value come from test experiments or, more likely,
from Monte Carlo simulations of the physics process and of the
detector. So we need to enlarge
the model adding four other nodes, taking into account
the probabilistic links
We refrain from adding the four nodes in the network
of Fig. ![[*]](crossref.png) , which will become more busy
in a while. Anyway, we can just assign to
, which will become more busy
in a while. Anyway, we can just assign to
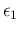 and
and
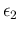 the parameter of the probability distribution
resulting from the inferences based on Monte Carlo simulations
(see Ref. [1] for details - remember that, having
the nodes
the parameter of the probability distribution
resulting from the inferences based on Monte Carlo simulations
(see Ref. [1] for details - remember that, having
the nodes
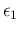 and
and
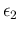 no parents, they need priors).
no parents, they need priors).
What is still missing in the model of Fig. ![[*]](crossref.png) is background. In fact, we do not only lose events
because of inefficiencies, but the `experimentally defined class'
can get contributions from other `physical class(es)'
(in general there are several physical classes contributing
as background). Figure
is background. In fact, we do not only lose events
because of inefficiencies, but the `experimentally defined class'
can get contributions from other `physical class(es)'
(in general there are several physical classes contributing
as background). Figure ![[*]](crossref.png) shows the extension
shows the extension
Figure:
Extended model of Fig. ![[*]](crossref.png) including also background.
including also background.
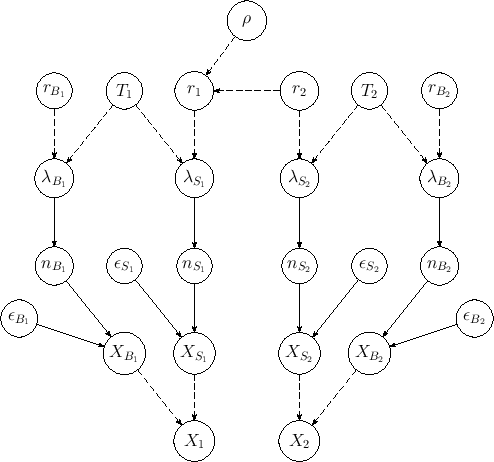 |
of the previous model, in which each Poisson process
which describes the signal has just one background Poisson process.
All variables have subscripts 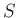 or
or 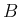 , depending if their
are associated to signal or background
(with exception of
, depending if their
are associated to signal or background
(with exception of 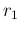 and
and 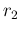 , which are obviously the two
signal rates). As before, the nodes needed to infer
the efficiencies are not shown in the diagram, which is therefore
missing eight `bubbles'.
, which are obviously the two
signal rates). As before, the nodes needed to infer
the efficiencies are not shown in the diagram, which is therefore
missing eight `bubbles'.
At this point it is clear that trying to achieve closed formulae
is out of hope, and we need to use other methods to perform the
integrals of interest,
namely those based on Markov Chain Monte Carlo. We show here how
to use a powerful package that does the work for
us. But we do it only for the two cases of which we already have
closed solutions in hand, that is the models of Figs. ![[*]](crossref.png) and
and ![[*]](crossref.png) starting from uniform priors
for the `top nodes'.
The program we are going to use is JAGS [36]
interfaced to R via the package jrags [37].
starting from uniform priors
for the `top nodes'.
The program we are going to use is JAGS [36]
interfaced to R via the package jrags [37].
 Introducing MCMC and related algorithms
goes well beyond the purpose of this paper
and we recommend Ref. [38] (some examples of application,
including R scripts, are also provided in
Ref. [1]).
Moreover, mentioning the Gibbs Sampler algorithm applied to
probabilistic inference (and forecasting) it is impossible
not to refer to the BUGS project [39],
whose acronym stands
for Bayesian inference using
Gibbs Sampler, that has
been a kind of revolution in Bayesian analysis,
decades ago limited to simple cases because of computational problems
(see also Sec. 1 of Ref.[36]).
In the BUGS project web site [40]
it is possible to find packages with excellent Graphical User Interface,
tutorials and many examples [41].
Introducing MCMC and related algorithms
goes well beyond the purpose of this paper
and we recommend Ref. [38] (some examples of application,
including R scripts, are also provided in
Ref. [1]).
Moreover, mentioning the Gibbs Sampler algorithm applied to
probabilistic inference (and forecasting) it is impossible
not to refer to the BUGS project [39],
whose acronym stands
for Bayesian inference using
Gibbs Sampler, that has
been a kind of revolution in Bayesian analysis,
decades ago limited to simple cases because of computational problems
(see also Sec. 1 of Ref.[36]).
In the BUGS project web site [40]
it is possible to find packages with excellent Graphical User Interface,
tutorials and many examples [41]. ![$]$](img192.png)
Subsections
![[*]](crossref.png) (hereafter we stick to this last model),
adding the relevant nodes.
(hereafter we stick to this last model),
adding the relevant nodes.
![[*]](crossref.png) ,
,
![[*]](crossref.png) , which will become more busy
in a while. Anyway, we can just assign to
, which will become more busy
in a while. Anyway, we can just assign to
![[*]](crossref.png) is background. In fact, we do not only lose events
because of inefficiencies, but the `experimentally defined class'
can get contributions from other `physical class(es)'
(in general there are several physical classes contributing
as background). Figure
is background. In fact, we do not only lose events
because of inefficiencies, but the `experimentally defined class'
can get contributions from other `physical class(es)'
(in general there are several physical classes contributing
as background). Figure ![[*]](crossref.png) shows the extension
shows the extension
![[*]](crossref.png) and
and ![[*]](crossref.png) starting from uniform priors
for the `top nodes'.
The program we are going to use is JAGS [36]
interfaced to R via the package jrags [37].
starting from uniform priors
for the `top nodes'.
The program we are going to use is JAGS [36]
interfaced to R via the package jrags [37].
![]() Introducing MCMC and related algorithms
goes well beyond the purpose of this paper
and we recommend Ref. [38] (some examples of application,
including R scripts, are also provided in
Ref. [1]).
Moreover, mentioning the Gibbs Sampler algorithm applied to
probabilistic inference (and forecasting) it is impossible
not to refer to the BUGS project [39],
whose acronym stands
for Bayesian inference using
Gibbs Sampler, that has
been a kind of revolution in Bayesian analysis,
decades ago limited to simple cases because of computational problems
(see also Sec. 1 of Ref.[36]).
In the BUGS project web site [40]
it is possible to find packages with excellent Graphical User Interface,
tutorials and many examples [41].
Introducing MCMC and related algorithms
goes well beyond the purpose of this paper
and we recommend Ref. [38] (some examples of application,
including R scripts, are also provided in
Ref. [1]).
Moreover, mentioning the Gibbs Sampler algorithm applied to
probabilistic inference (and forecasting) it is impossible
not to refer to the BUGS project [39],
whose acronym stands
for Bayesian inference using
Gibbs Sampler, that has
been a kind of revolution in Bayesian analysis,
decades ago limited to simple cases because of computational problems
(see also Sec. 1 of Ref.[36]).
In the BUGS project web site [40]
it is possible to find packages with excellent Graphical User Interface,
tutorials and many examples [41]. ![]()