Inferred distribution of 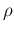
Let us start with pdf of 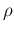 . Our starting point is
. Our starting point is
from which it follows
in which we have explicitly factorized 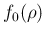 .
Again, besides
.
Again, besides 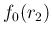 , we recognize in the integrand
something proportional to a Gamma pdf. If we then
model also
, we recognize in the integrand
something proportional to a Gamma pdf. If we then
model also 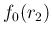 by a Gamma of parameters
by a Gamma of parameters 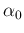 and
and 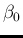 ,
and again neglect
irrelevant factors, we get
,
and again neglect
irrelevant factors, we get
Indicating, in analogy to what done to obtain
Eq. (![[*]](crossref.png) ),
the power of
),
the power of 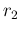 as
as
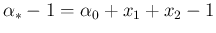 , and the factor multiplying
, and the factor multiplying 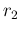 at the exponent
as
at the exponent
as
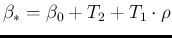 , we get
, we get
What is interesting with this result is that we can
consider the term inside the square brackets as an effective likelihood
(remember that multiplicative factors are irrelevant),
and therefore we can rewrite Eq. (![[*]](crossref.png) ) as
) as
For this reason we can serenely proceed assuming
a flat prior about 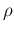 , because we can reshape
in a second step the result (see Ref. [1] for details).
So, assuming
, because we can reshape
in a second step the result (see Ref. [1] for details).
So, assuming
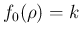 and comparing the expression inside the square bracket
of Eq. (
and comparing the expression inside the square bracket
of Eq. (![[*]](crossref.png) )
with
Eq. (
)
with
Eq. (![[*]](crossref.png) ) we get
the normalization just by analogy, thus getting
) we get
the normalization just by analogy, thus getting
or
that, for a flat prior about 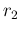 , i.e.
, i.e.
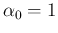 and
and 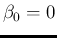 , becomes
, becomes
The comparison of this result with
Eq. (![[*]](crossref.png) ),
obtained using flat priors for
),
obtained using flat priors for 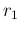 and
and 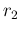 ,
is at least surprising: the structures of the pdf's are the same,
but
,
is at least surprising: the structures of the pdf's are the same,
but 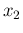 in Eq. (
in Eq. (![[*]](crossref.png) )
is replaced by
)
is replaced by 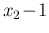 in Eq. (
in Eq. (![[*]](crossref.png) ).
Obviously, the two results will coincide for large
).
Obviously, the two results will coincide for large 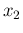 ,
and also for small
,
and also for small 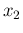 there is not a dramatic
difference, as we can see from Fig.
there is not a dramatic
difference, as we can see from Fig. ![[*]](crossref.png) .
.
Figure:
Dependence of the inference of 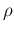 from the
priors. Solid lines: flat priors on
from the
priors. Solid lines: flat priors on 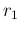 and
and 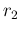 , as in
Figs.
, as in
Figs. ![[*]](crossref.png) and
and ![[*]](crossref.png) ,
following from the causal model depicted in Fig.
,
following from the causal model depicted in Fig. ![[*]](crossref.png) .
Dashed lines: flat priors on
.
Dashed lines: flat priors on 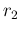 and
and 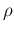 (causal model of Fig.
(causal model of Fig. ![[*]](crossref.png) .)
.)
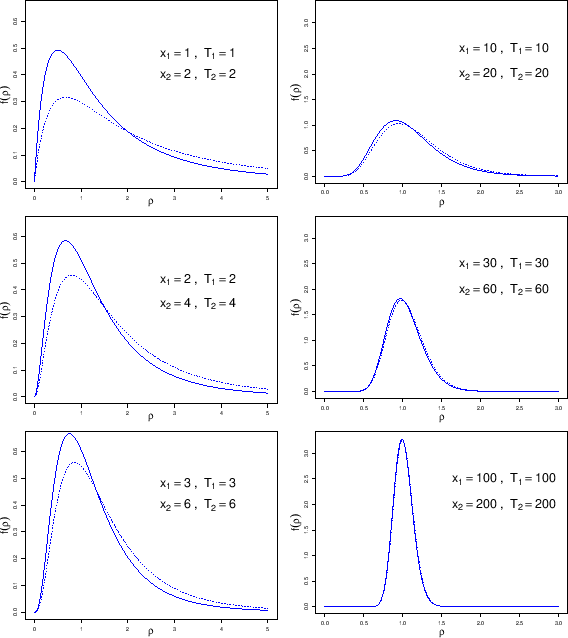 |
As far as the summaries of the distribution are concerned, we get
At this point, instead of taking comfort for the fact that
the differences are irrelevant in practical cases,
or tout court `rejecting Bayesian methods because
of their dependence of priors', it is interesting to try
to understand the origin of this effect,
certainly related to the priors.
But, before proceeding, let
us not forget that Eq. (![[*]](crossref.png) )
was obtained
assuming a flat prior about
)
was obtained
assuming a flat prior about 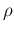 and that in that model
this prior can be factorized.
Therefore the more general pdf of the rate ratio for the model of
Fig.
and that in that model
this prior can be factorized.
Therefore the more general pdf of the rate ratio for the model of
Fig. ![[*]](crossref.png) is
is
having only the limitation (but in reality almost irrelevant, given
the flexibility of the Gamma distribution) of depending
on the chosen parametrization for 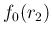 .
.
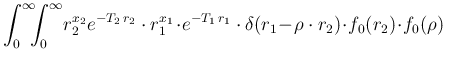 d
d![$\displaystyle \left[ \int_0^\infty\!
r_2^{x_2} e^{-T_2\,r_2}
\cdot (\rho\cdot r...
...dot\! e^{-T_1\,\rho\,r_2}\cdot
f_0(r_2)\, \mbox{d}r_2 \right] \cdot\! f_0(\rho)$](img388.png)
![$\displaystyle \left[\, \rho^{x_1}\cdot
\int_0^\infty\! r_2^{x_1+x_2}\cdot e^{-(...
...1\cdot\rho)\cdot r_2}\cdot f_0(r_2)
\, \mbox{d}r_2 \right] \cdot\! f_0(\rho)\,,$](img389.png)
![$\displaystyle \left[\, \rho^{x_1}\cdot
\int_0^\infty\! r_2^{x_1+x_2}\cdot e^{-(...
...pha_0-1}
\cdot e^{-\beta_0\,r_2}
\, \mbox{d}r_2 \right] \cdot\! f_0(\rho)\ \ \ $](img392.png)
![$\displaystyle \left[\, \rho^{x_1}\cdot
\int_0^\infty\! r_2^{\alpha_0+x_1+x_2-1}...
...eta_0+T_2+T_1\cdot\rho)\cdot r_2}
\, \mbox{d}r_2\, \right] \cdot\! f_0(\rho)\,.$](img393.png)
![[*]](crossref.png) ),
the power of
),
the power of ![[*]](crossref.png) ) as
) as
![[*]](crossref.png) )
with
Eq. (
)
with
Eq. (![[*]](crossref.png) ) we get
the normalization just by analogy, thus getting
) we get
the normalization just by analogy, thus getting
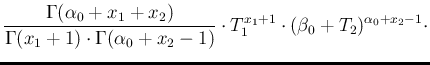
![[*]](crossref.png) ),
obtained using flat priors for
),
obtained using flat priors for ![[*]](crossref.png) )
is replaced by
)
is replaced by ![[*]](crossref.png) ).
Obviously, the two results will coincide for large
).
Obviously, the two results will coincide for large ![[*]](crossref.png) .
.
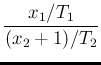

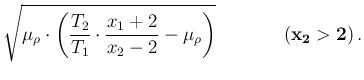
![[*]](crossref.png) )
was obtained
assuming a flat prior about
)
was obtained
assuming a flat prior about ![]() and that in that model
this prior can be factorized.
Therefore the more general pdf of the rate ratio for the model of
Fig.
and that in that model
this prior can be factorized.
Therefore the more general pdf of the rate ratio for the model of
Fig. ![[*]](crossref.png) is
is