Inferring  , having observed
, having observed 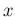 counts in
the measuring time
counts in
the measuring time 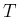
Being  equal to
equal to 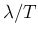 , we can obtain its pdf
by a simple change of variables.18But, having practiced a bit with the Gamma distribution, we can reach
the identical result observing that, using again a flat prior and
neglecting irrelevant factors, the pdf of
, we can obtain its pdf
by a simple change of variables.18But, having practiced a bit with the Gamma distribution, we can reach
the identical result observing that, using again a flat prior and
neglecting irrelevant factors, the pdf of  is given by
is given by
in which we recognize, besides the normalization factor,
a Gamma pdf for the variable  with
with
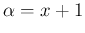 and
and 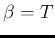 , and hence
, and hence
Mode, expected value and standard deviation of  are then
(see Appendix A)
are then
(see Appendix A)
as also expected from the `summaries' of
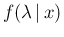 and making use of
and making use of
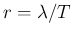 .
.
 Note that the pdf (
Note that the pdf (![[*]](crossref.png) )
assumes, as explicitly written in the condition, a precise
value of
)
assumes, as explicitly written in the condition, a precise
value of 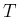 . If this is not the case and
. If this is not the case and 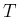 is uncertain, then,
similarly to what we have seen in footnote
is uncertain, then,
similarly to what we have seen in footnote
![[*]](crossref.png) ,
the pdf of
,
the pdf of  is evaluated as
is evaluated as
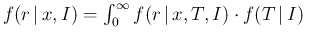 d
d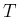 .
. ![$]$](img192.png)
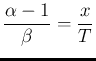
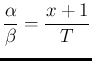
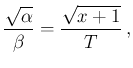
![[*]](crossref.png) )
assumes, as explicitly written in the condition, a precise
value of
)
assumes, as explicitly written in the condition, a precise
value of ![[*]](crossref.png) ,
the pdf of
,
the pdf of