Inferring $r_1$ and $r_2$ ($T_1$ possibly different from $T_2$)

After having been playing with $\lambda$'s and their ratios, from which we started for simplicity, let us move now to the rates $r_1$ and $r_2$ of the two Poisson processes, i.e. to the case in which the observation times $T_1$ and $T_2$ might be different.

But, before doing that, let us spend a few words on the reason of the word `deducing', appearing in the title of the previous section. Let us start framing what we have been doing in the past section in the graphical model of Fig. , known as a Bayesian network (the reason for the adjective will be clear in the sequel).

Figure: Graphical model showing the model underlying the inference of $\lambda_1$ and $\lambda_2$ from the observed numbers of counts $X_1$ and $X_2$, followed by the deduction of $\rho$.

The solid arrows from the nodes $\lambda_i$ to the nodes $X_i$ indicate that the effect $X_i$ is caused by $\lambda_i$, although in a probabilistic way (more properly, $X_i$ is conditioned by $\lambda_i$, since, as it is well understood causality is a tough concept¹⁶). The dashed arrows indicate, instead, deterministic links (or deterministic `cause-effect' relations, if you wish). For this reason we have been talking about `deduction': each couple of values $(\lambda_1,\lambda_2)$ provides a unique value of $\rho_\lambda$, equal to $\lambda_1/\lambda_2$, and any uncertainty about the $\lambda$'s is `directly propagated' into uncertainty about $\rho_\lambda$. The same will happen with $\rho=r_1/r_2$.

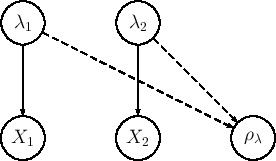Navigating back along the solid arrows, that is from $X_i$ to $\lambda_i$, is often called a problem of `inverse probability', although nowadays many experts do not like this expression, which however gives an idea of what is going on. More precisely, it is an inferential problem, notoriously tackled for the first time in mathematical terms by Thomas Bayes [19] and Simon de Laplace, who was indeed talking about “la probabilité des causes par les événements”[20]. Nowadays the probabilistic tool to perform this `inversion' goes under the name of Bayes' theorem, or Bayes' rule, whose essence, in terms of the possible causes $C_i$ of the observed effect $E$, is given, besides normalization, by this very simple formula

$$P(C_i\,\vert\,E,I) \propto P(E\,\vert\,C_i,I)\cdot P(C_i\,\vert\,I)\,,$$ (27)

having indicated again by $I$ the background state of information. $P(C_i\,\vert\,I)$ quantifies our belief that $C_i$ is true taking into account all available information, except for $E$. If also the hypothesis that $E$ is occurred is considered to be true,¹⁷then the `prior' $P(C_i\,\vert\,I)$ is turned into the `posterior' $P(C_i\,\vert\,E,I)$.

We shall came back on the question of the priors, but now let us move to infer $r_1$, $r_2$ and their ratio $\rho=r_1/r_2$.