



Next: Incertezze note e diverse
Up: Esempi di applicazione delle
Previous: Esempi di applicazione delle
Indice
Questo è sicuramente il caso più interessante
per le applicazioni di laboratorio. Infatti non sempre
è possibile valutare le deviazioni standard associate
agli errori casuali ripetendo molte volte le misure a parità
di condizioni. Inoltre anche ripetendo le misure si potrebbe
non tenere conto di possibili fluttuazioni che dipendono
dal valore del misurando (vedi discussione sugli errori sistematici,
paragrafo 12.7, primo punto).
Come esempio numerico,
consideriamo i dati dell'allungamento della molla
in funzione della massa applicata
(vedi tabella 2.5).
Si noti l'assenza, a questo livello, di incertezze associate
alle misure. Infatti ogni stima sarebbe arbitraria, come discusso
lungamente nei capitoli precedenti. I valori
sono stati riportati con tutte le cifre che si riuscivano ad
apprezzare sugli strumenti. Si noti
come gli studenti abbiano deciso,
nonostante le raccomandazioni contrarie,
che, date le condizioni di lavoro,
fosse difficile effettuare letture al di sotto del millimetro.
Vedremo nel seguito
se, con il senno del poi, avrebbero dovuto sforzarsi un po'
e quali sono le conseguenze
sul risultato.
Riportiamo
nella tabella
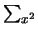 i dettagli
dei calcoli. I simboli
i dettagli
dei calcoli. I simboli 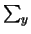 ,
,
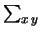 ,
, 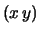 ,
,
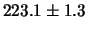 stanno per le sommatorie di interesse.
stanno per le sommatorie di interesse.
Tabella:
Dettagli del fit dei dati dell'allungamento della molla.
| |
|
|
|
|
| |
Serie 1 |
Serie 2 |
Serie 3 |
Media |
| |
|
|
|
|
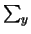 (kg) (kg) |
4.607 |
4.607 |
4.607 |
4.607 |
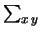 (kg (kg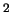 ) ) |
2.914 |
2.914 |
2.914 |
2.914 |
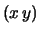 (mm) (mm) |
605 |
617 |
619 |
613.67 |
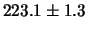 (kg (kg mm) mm) |
406.6 |
413.4 |
414.6 |
411.6 |
| |
|
|
|
|
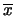 (kg) (kg) |
0.5758 |
0.5758 |
0.5758 |
0.5758 |
 (kg (kg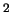 ) ) |
0.3642 |
0.3642 |
0.3642 |
0.3642 |
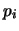 (mm) (mm) |
75.63 |
77.13 |
77.38 |
76.71 |
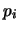 (kg (kg mm) mm) |
50.83 |
51.68 |
51.82 |
51.44 |
| |
|
|
|
|
Var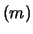 |
0.03262 |
0.03262 |
0.03262 |
.03262 |
Cov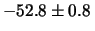 |
7.276 |
7.266 |
7.2663 |
7.269 |
| |
|
|
|
|
 (mm/kg) (mm/kg) |
223.1 |
222.77 |
222.77 |
222.88 |
 (mm) (mm) |
-52.84 |
-51.17 |
-50.91 |
-51.64 |
| |
|
|
|
|
 (mm) (mm) |
0.659 |
0.319 |
0.569 |
0.290 |
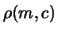 (mm/kg) (mm/kg) |
1.291 |
0.624 |
1.11 |
0.567 |
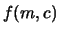 (mm) (mm) |
0.779 |
0.377 |
0.672 |
0.342 |
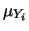 |
-0.954 |
-0.954 |
-0.954 |
-0.954 |
| |
|
|
|
|
|
Si noti come il numero di cifre della tabella non è legato
alle regole sulle cifre significative, secondo le raccomandazioni
che durante i conti è meglio portarsi dietro molte cifre (vedi
ad esempio nota al paragrafo 5.14). I risultati
finali si danno invece secondo le regole. Ad esempio, per la 1.a serie:
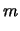 |
 |
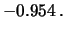 mm/kg mm/kg |
(12.12) |
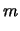 |
 |
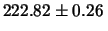 mm mm |
(12.13) |
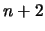 |
 |
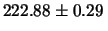 |
(12.14) |
Si noti inoltre come il coefficiente di correlazione non
sia un optional, ma faccia parte integrante del risultato
(vedi anche 12.5 e
discussione nel paragrafo 12.8,
in particolare punti 8 e 10).
La quarta colonna della tabella è ottenuta utilizzando
gli allungamenti medi.
Si noti come l'informazione sui parametri che si ottiene mediando le tre
serie di misure è approssimativamente uguale
(sia come valore che come deviazione standard) a quella combinando
direttamente i tre risultati. Ad esempio la media dei tre valori
di 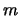 è pari a
è pari a
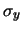 mm/kg, contro
mm/kg, contro
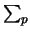 mm/kg ottenuto dagli allungamenti medi.
mm/kg ottenuto dagli allungamenti medi.




Next: Incertezze note e diverse
Up: Esempi di applicazione delle
Previous: Esempi di applicazione delle
Indice
Giulio D'Agostini
2001-04-02
![]() i dettagli
dei calcoli. I simboli
i dettagli
dei calcoli. I simboli ![]() ,
,
![]() ,
, ![]() ,
,
![]() stanno per le sommatorie di interesse.
stanno per le sommatorie di interesse.
![]() è pari a
è pari a
![]() mm/kg, contro
mm/kg, contro
![]() mm/kg ottenuto dagli allungamenti medi.
mm/kg ottenuto dagli allungamenti medi.