



Next: Misure di dispersione e
Up: Descrizione quantitativa dei dati
Previous: Effetto del raggruppamento in
Indice
Dispersione relativa e
coefficiente di variazione
Gli istogrammi di figura 4.2 mostrano un chiaro
allargamento della distribuzioni in funzione del tempo.
Questo può essere quantificato con le misure di dispersione
viste nel paragrafo 5.4. Però,
come è noto dalla vita quotidiana, la dispersione assoluta
non è sempre il miglior criterio per stabilire se ci sono fluttuazioni
rispetto ai valori tipici. Immaginiamo che una indagine mostri che
il prezzo di una scatola di pelati sia intorno a 800 lire, ma con un
campo di variazione compreso fra 400 e 1500 lire, mentre lo champagne
varia fra 32 000 e
45
000 e
45 000 lire con un prezzo medio di 40
000 lire con un prezzo medio di 40 000.
Si concorderà nel dire che le fluttuazioni sul prezzo dei pelati
è superiore di quello dello champagne sebbene il campo di variabilità
di quest'ultimo sia di un ordine di grandezza superiore a quello
dei pelati (se i prezzi di una moto variano al più di 10
000.
Si concorderà nel dire che le fluttuazioni sul prezzo dei pelati
è superiore di quello dello champagne sebbene il campo di variabilità
di quest'ultimo sia di un ordine di grandezza superiore a quello
dei pelati (se i prezzi di una moto variano al più di 10 000 lire
da un concessionario all'
altro, diciamo, giustamente, che sono ``esattamente uguali'').
Infatti, spesso siamo interessati alle fluttuazioni relative.
Esse sono usualmente quantificate in termini della dispersione rapportata
ai valori tipici ed è immaginabile pensare alla grande varietà
di modi con cui può essere espressa la dispersione relativa.
Accenniamo soltanto al coefficiente di variazione, definito
a partire da media e deviazione standard:
000 lire
da un concessionario all'
altro, diciamo, giustamente, che sono ``esattamente uguali'').
Infatti, spesso siamo interessati alle fluttuazioni relative.
Esse sono usualmente quantificate in termini della dispersione rapportata
ai valori tipici ed è immaginabile pensare alla grande varietà
di modi con cui può essere espressa la dispersione relativa.
Accenniamo soltanto al coefficiente di variazione, definito
a partire da media e deviazione standard:
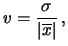 |
(5.35) |
espressa a volte anche in percentuale. Il modulo serve a rendere tale
misura di larghezza relativa
indipendente dal segno della media (come lo è già
la deviazione standard).
Ad esempio, la distribuzione
dei conteggi per  s ha un coefficiente di variazione pari 1.35,
o del 135%, mentre quella per
s ha un coefficiente di variazione pari 1.35,
o del 135%, mentre quella per 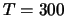 s lo ha del 14%.
Si dice quindi che la seconda distribuzione è relativamente più
stretta
della prima.
s lo ha del 14%.
Si dice quindi che la seconda distribuzione è relativamente più
stretta
della prima.




Next: Misure di dispersione e
Up: Descrizione quantitativa dei dati
Previous: Effetto del raggruppamento in
Indice
Giulio D'Agostini
2001-04-02