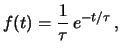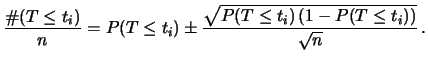Next: Limite a poissoniana della
Up: Contatore e processo di
Previous: Distribuzione di Poisson
Indice
Occupiamoci ora dell'intervalli di tempo
che intercorre fra due conteggi successivi, ovvero
del tempo di attesa per registrare un conteggio a partire
da un istante arbitrario. Si tratta di un numero aleatorio continuo
descritto da una distribuzione esponenziale negativa
con
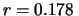 s
s . Più comunemente è scritta
in termini di
. Più comunemente è scritta
in termini di 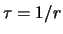 come
con
come
con
 s.
Da questa distribuzione possiamo derivare tutte le affermazioni
probabilistiche di interesse.
s.
Da questa distribuzione possiamo derivare tutte le affermazioni
probabilistiche di interesse.
- Previsione e incertezza di previsione valgono
quindi ci aspettiamo grandi fluttuazioni dei tempi osservati.
- Fissati dei valori di tempo, ad esempio 1, 2, 4, 10 e 20
secondi, possiamo calcolare le probabilità di osservare
un tempo di attesa inferiore o uguale ad essi
- Se ripetiamo l'esperimento
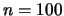 volte ci aspettiamo che il
numero di volte che si osserveranno
tempi di attesa inferiori a
volte ci aspettiamo che il
numero di volte che si osserveranno
tempi di attesa inferiori a 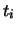 sia
(usando la notazione ``previsione
sia
(usando la notazione ``previsione  incertezza di previsione'')
ovvero frequenze relative
Otteniamo, ad esempio:
incertezza di previsione'')
ovvero frequenze relative
Otteniamo, ad esempio:
le quali, essendo 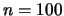 corrispondono anche alle frequenze relative
espresse in percentuali.
corrispondono anche alle frequenze relative
espresse in percentuali.
È interessante confrontare queste previsioni con quanto ``osservato''
nell'esperimento simulato (vedi tabelle 1.2
e 5.1). Il numero di volte che si è verificato un
tempo di attesa inferiore a 1, 2, 4, 10 e 20 secondi è, rispettivamente:
19, 30, 50, 83 e 99, in ``ottimo accordo'' con le
previsioni.
A questo punto è importante notare
come i dati simulati non siano stati
minimamente truccati o, per dire la stessa cosa con un
eufemismo, ``filtrati per ragioni didattiche''.
Il fatto è che è semplicemente
molto poco probabile ottenere distribuzioni di frequenze relative
che si discostano molto dalla distribuzione di probabilità
e pertanto sarebbe stato ``sorprendente'' non osservare
una distribuzione non in accordo, entro le incertezze di previsione,
con le previsioni stesse.




Next: Limite a poissoniana della
Up: Contatore e processo di
Previous: Distribuzione di Poisson
Indice
Giulio D'Agostini
2001-04-02