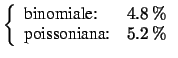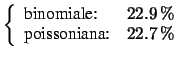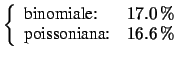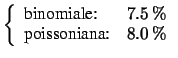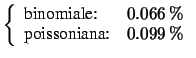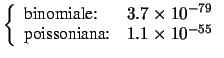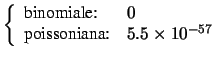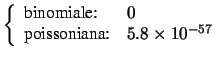Next: pzd100Contatore e distribuzione Gamma
Up: Previsioni dei risultati
Previous: Distribuzione esponenziale
Indice
Quando una distribuzione binomiale ha 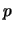 ``molto piccolo'' e
``molto piccolo'' e
 ``molto grande'', la funzione di probabilità non dipende
dai due parametri
``molto grande'', la funzione di probabilità non dipende
dai due parametri  e
e 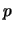 separatamente, ma soltanto dalla
combinazione
separatamente, ma soltanto dalla
combinazione 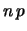 , pari al valore atteso, purché questo sia,
ovviamente finito.
Come primo esempio, supponiamo di far scendere 10000
palline in un pallinometro a 32 file di chiodi. Quante palline
arriveranno nella celletta numero 7 (
, pari al valore atteso, purché questo sia,
ovviamente finito.
Come primo esempio, supponiamo di far scendere 10000
palline in un pallinometro a 32 file di chiodi. Quante palline
arriveranno nella celletta numero 7 (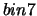 )?
La probabilità che una singola pallina cada in tale celletta
è pari a
)?
La probabilità che una singola pallina cada in tale celletta
è pari a
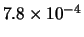 (vedi formula (7.2)
e tabella 7.5).
Quindi il numero aleatorio di interesse segue
una distribuzione binomiale avente
(vedi formula (7.2)
e tabella 7.5).
Quindi il numero aleatorio di interesse segue
una distribuzione binomiale avente
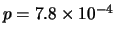 ,
,
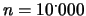 ,
valore atteso 7.8 e deviazione standard 2.8. Come si vede,
le condizioni di
,
valore atteso 7.8 e deviazione standard 2.8. Come si vede,
le condizioni di 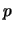 molto piccolo,
molto piccolo,  molto grande e
molto grande e 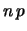 finito
sono soddisfatte e quindi lo stesso numero è descritto
abbastanza bene da una poissoniana di
finito
sono soddisfatte e quindi lo stesso numero è descritto
abbastanza bene da una poissoniana di
 .
Riportiamo, nella tabella 7.4
.
Riportiamo, nella tabella 7.4
Tabella:
Confronto fra alcuni valori
della distribuzione binomiale e la distribuzione
di Poisson che la approssima.
| X |
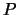 binomiale binomiale |
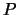 poissoniana poissoniana |
| |
(
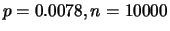 ) ) |
(
 ) ) |
| |
|
|
| 0 |
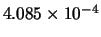 |
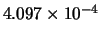 |
| 1 |
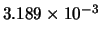 |
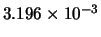 |
| 2 |
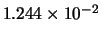 |
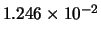 |
| ... |
|
|
| 7 |
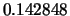 |
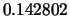 |
| 8 |
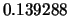 |
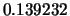 |
| 9 |
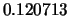 |
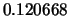 |
| ... |
|
|
| 20 |
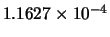 |
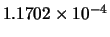 |
| ... |
|
|
| 50 |
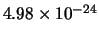 |
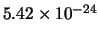 |
| ... |
|
|
| 100 |
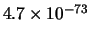 |
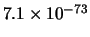 |
| ... |
|
|
| 1000 |
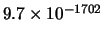 |
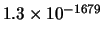 |
| ... |
|
|
| 10000 |
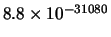 |
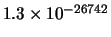 |
| 10001 |
0 |
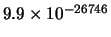 |
| |
|
|
|
il confronto fra la distribuzione binomiale e la distribuzione di
Poisson che l'approssima. Si noti come, con i parametri dell'esempio,
l'accordo sia ottimo per piccoli valori della variabile e
si mantiene ragionevole addirittura oltre la decina di
deviazioni standard dal valore atteso. Quando 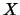 diventa confrontabile
con
diventa confrontabile
con  l'approssimazione è naturamente pessima.
l'approssimazione è naturamente pessima.
Come secondo esempio consideriamo ora
il caso del lancio di 30 palline in un
pallinometro a due file di chiodi. Interessiamoci
all'evento 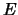 ``il numero di palline che cadono
nel bin centrale (
``il numero di palline che cadono
nel bin centrale (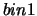 ) è minore uguale a 10''.
Dalla tabella 7.1 calcoliamo la probabilità
di tale evento:
) è minore uguale a 10''.
Dalla tabella 7.1 calcoliamo la probabilità
di tale evento:
Immaginiamo ora che 60 studenti eseguano tale esperimento
e siamo interessati al numero di studenti ai quali accada l'evento 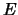 .
Indichiamo con
.
Indichiamo con 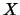 questo nuovo numero aleatorio. Esso è descritto
da una distribuzione binomiale avente
questo nuovo numero aleatorio. Esso è descritto
da una distribuzione binomiale avente
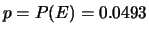 e
e  .
Quindi:
.
Quindi:
Date le condizioni, 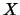 può essere descritta con buona approssimazione
da una poissoniana di
può essere descritta con buona approssimazione
da una poissoniana di
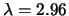 :
:
Per confronto, calcoliamo la probabilità che
a nessuno studente capiti tale evento, che esso capiti
ad esattamente due studenti, a quattro, a più di cinque
e ad almeno 10:
Come si vede, le probabilità sono praticamente uguali intorno al centro
della distribuzione, mentre, naturalmente, tendono a differire molto
sulle code. In particolare, si ricordi come la variabile casuale
di una distribuzione binomiale può assumere valori fino a  , mentre
per la distribuzione di Poisson non c'è alcun limite. Quindi nel nostro caso:
, mentre
per la distribuzione di Poisson non c'è alcun limite. Quindi nel nostro caso:




Next: pzd100Contatore e distribuzione Gamma
Up: Previsioni dei risultati
Previous: Distribuzione esponenziale
Indice
Giulio D'Agostini
2001-04-02
![]() ``il numero di palline che cadono
nel bin centrale (
``il numero di palline che cadono
nel bin centrale (![]() ) è minore uguale a 10''.
Dalla tabella 7.1 calcoliamo la probabilità
di tale evento:
) è minore uguale a 10''.
Dalla tabella 7.1 calcoliamo la probabilità
di tale evento: