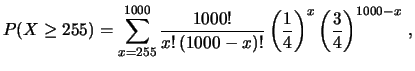 |
(7.12) |
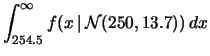 |
|||
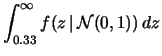 |
|||
Per esercitarci ancora a fare ginnastica fra le varie distribuzioni,
calcoliamo previsione e incertezza di previsione del numero
di volte che almeno 255 palline su 1000 cadono in una celletta laterale,
se l'esperimento viene ripetuto, come nella tabella 1.3
per 10 volte. Di nuovo abbiamo a che fare con 10 processi di Bernoulli
indipendenti, ciascuno di probabilità 0.37 (arrotondiamo per non
perderci dietro i dettagli numerici).
Ci aspettiamo quindi che questo si verifichi
![]() volte.
Il risultato dell'esperimento simulato è 3 volte se
si considera il bin 0 e 2 volte se si considera il bin 1
(si faccia attenzione al fatto che il numero di palline nelle due cellette
sono correlati!). Ancora una volta l'accordo è buono e ancora
una volta invitiamo a non dare nessun significato
``metafisico'' (nel senso negativo del termine) o
scaramantico al fatto di aver osservato
qualcosa che aveva alta probabilità di accadere.
volte.
Il risultato dell'esperimento simulato è 3 volte se
si considera il bin 0 e 2 volte se si considera il bin 1
(si faccia attenzione al fatto che il numero di palline nelle due cellette
sono correlati!). Ancora una volta l'accordo è buono e ancora
una volta invitiamo a non dare nessun significato
``metafisico'' (nel senso negativo del termine) o
scaramantico al fatto di aver osservato
qualcosa che aveva alta probabilità di accadere.
Come secondo esempio di tendenza della binomiale a normale e
sempre con riferimento
al pallinometro, calcoliamo la probabilità che una pallina cada in
una certa celletta se abbiamo un pallinometro a molte file di chiodi,
ad esempio 32 file, che è una delle massime configurazioni ottenibili
con il pallinometro simulato a disposizione degli studenti a Roma.
La variabile ![]() = ``numero di celletta'' può andare da 0 a 32
ed è distribuita secondo una binomiale di
= ``numero di celletta'' può andare da 0 a 32
ed è distribuita secondo una binomiale di ![]() e
e ![]() , con
valore atteso 16 e deviazione standard 2.8. Calcoliamo la
probabilità con la formula esatta o usando l'approssimazione
a normale. Inoltre calcoliamo la previsione del numero di palline
che terminano nelle varie cellette se lanciamo in totale
, con
valore atteso 16 e deviazione standard 2.8. Calcoliamo la
probabilità con la formula esatta o usando l'approssimazione
a normale. Inoltre calcoliamo la previsione del numero di palline
che terminano nelle varie cellette se lanciamo in totale
![]() o
o
![]() di palline.
Per queste ultime è riportato il conto esatto e non
quello approssimato.
I risultati sono riportati in tabella 7.5
di palline.
Per queste ultime è riportato il conto esatto e non
quello approssimato.
I risultati sono riportati in tabella 7.5