



Next: Inferenza probabilistica su
Up: Un esempio storico di
Previous: Stima ``puntuale'' del parametro
Indice
Estendiamo ora le previsioni a 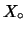 ipotetici reggimenti reggimenti che si comportino
in quel modo
(ma diversi dai 200 osservati).
In quanti ci aspettiamo che
non si verifica nessun morto? Se indichiamo con
ipotetici reggimenti reggimenti che si comportino
in quel modo
(ma diversi dai 200 osservati).
In quanti ci aspettiamo che
non si verifica nessun morto? Se indichiamo con
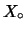 la variabile casuale ``numeri di volte in cui si registra
nessun morto'', questa sarà distribuita secondo una binomiale:
la variabile casuale ``numeri di volte in cui si registra
nessun morto'', questa sarà distribuita secondo una binomiale:
Ne segue che
ci aspettiamo di trovare 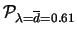 reggimenti su 200 in non
si verifichi alcun morto in un anno. La tabella 7.6
riporta un valore di 109. Un caso di accordo perfetto al quale
non va attribuito nessun significato particolare (se
qualche ombra di dubbio
che i dati siano stati truccati...). Riportiamo nella tabella
7.7 i dati originali, accompagnati dalle
previsioni e incertezze di previsioni subordinate ad un processo
di Poisson di
reggimenti su 200 in non
si verifichi alcun morto in un anno. La tabella 7.6
riporta un valore di 109. Un caso di accordo perfetto al quale
non va attribuito nessun significato particolare (se
qualche ombra di dubbio
che i dati siano stati truccati...). Riportiamo nella tabella
7.7 i dati originali, accompagnati dalle
previsioni e incertezze di previsioni subordinate ad un processo
di Poisson di
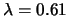 .
.
Tabella:
Confronto fra dati sperimentali e previsioni
calcolate assumendo un processo di Poisson con
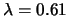 .
.
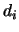 indica il numero di morti in un anno,
indica il numero di morti in un anno, 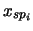 il numero
di occorrenze osservate sperimentalmente,
il numero
di occorrenze osservate sperimentalmente, 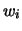 la frequenza
relativa delle occorrenze;
la frequenza
relativa delle occorrenze; 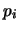 è la probabilità di
è la probabilità di 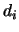 subordinata ad un processo di Poisson con
subordinata ad un processo di Poisson con
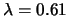 ;
;
 rappresenta il numero di occorrenze della
rappresenta il numero di occorrenze della
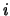 -ma possibilità e
-ma possibilità e 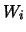 la rispettiva frequenza relativa.
la rispettiva frequenza relativa.
| |
|
|
|
| |
dati sperimentali |
previsioni basate su
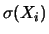 |
| |
|
|
|
| |
|
|
su 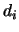 |
sulle frequenze di 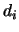 |
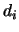 |
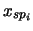 |
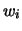 |
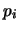 |
E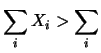 |
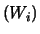 |
E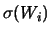 |
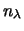 |
| |
|
(%) |
(%) |
|
|
(%) |
(%) |
| |
|
|
|
|
|
|
|
| 0 |
109 |
54.5 |
54.3 |
108.6 |
7.0 |
54.3 |
3.5 |
| 1 |
65 |
32.5 |
33.1 |
66.2 |
6.7 |
33.1 |
3.4 |
| 2 |
22 |
11.0 |
10.1 |
20.2 |
4.3 |
10.1 |
2.1 |
| 3 |
3 |
1.5 |
2.1 |
4.2 |
2.0 |
2.1 |
1.0 |
| 4 |
1 |
0.5 |
0.3 |
0.6 |
0.8 |
0.3 |
0.4 |
 |
0 |
0 |
0.04 |
0.1 |
0.3 |
0.04 |
0.2 |
| |
|
|
|
|
|
|
|
|
Si noti l'ottimo accordo fra dati e previsioni (entro le incertezze
di queste ultime).
Questo esempio, oltre alla funzione propedeutica
alla problematica della
``verifica''7.6 delle leggi statistiche, rappresenta anche un interessante caso
di una quantità calcolata mediante una distribuzione di probabilità
(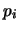 )
che viene successivamente
usata come parametro di un'altra distribuzione.
)
che viene successivamente
usata come parametro di un'altra distribuzione.
Subsections




Next: Inferenza probabilistica su
Up: Un esempio storico di
Previous: Stima ``puntuale'' del parametro
Indice
Giulio D'Agostini
2001-04-02
![]() )
che viene successivamente
usata come parametro di un'altra distribuzione.
)
che viene successivamente
usata come parametro di un'altra distribuzione.