Il corso sarà di 40 ore, con inizio 21 gennaio 2009,

Programma

• Programma indicativo.
• Per ulteriori dettagli, vedi il corso tenuto per il 22.mo Ciclo.

Orario

Calendario dettagliato
Att: Aggiornamento parziale ad uso di eventuali assenti alle lezioni (spero di riordinare/completare quanto prima...)
 

Nr.	Giorno	Orario	Aula
1	Mer 21/01	17:00-18:30	4
2	Gio 22/01	17:00-18:30	4
3	Mer 11/02	17:00-18:30	4
4	Gio 12/02	17:00-18:30	4
5	Mer  18/02	17:00-18:30	4
6	Gio  19/02	17:00-18:30	4
5	Mer  25/02	17:00-18:30	4
6	Gio  26/02	17:00-18:30	4
...	...	17:00-18:30	4
...	...	17:00-18:30	4

Dettaglio degli argomenti delle lezioni

Lezione 1 (21/1/09)

Introduzione: intento del corso e programma di massima.
'Task of the physicist': osservazioni -> ipotesi => incertezza.
Sorgenti di incertezza secondo la Guida ISO (il 'decalogo'). Trattazione usuali di incertezze: 'errori statistici' -> intervalli di confidenza; 'errori sistematici' -> ? -> regole ad hoc.
Rassegna critica di alcune conoscenze standard ('Fisichetta'): concetto e propagazione di `errori massimi'; semidispersione massima; uso della propagazione di `errori statistici'; regola della mezza divisione (errore di lettura? errore sistematico?); barre di errore calcolate dalle sole osservazioni; rette di massima e minima pendenza; significato di 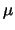=  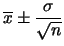 (oppure = ?).
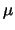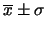Conclusioni su inadeguadezza errori massimi e difficoltà di uso degli 'errori statistici' nel quadro della statistica 'convenzionale' (frequentista).
Discussione sul significato di 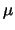=  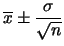: inversione intuitiva della probabilità e metafora cane-cacciatore.
Referimenti

• GdA, Errori e incertezze di misura - Rassegna critica e proposte per l'insegnamento (vedi qui), pp. 7-23 e 82-84.
• J. D. Mollon, A. J. Perkins, Errors of judgement at Greenwich in 1796, Nature 380, 101 - 102 (14 Mar 1996).
• Ole Rømer e la sua misura della velocità della luce
• Dava Sobel, Longitude.
• GdA, Bayesian reasoning in data analysis - A critical introduction (vedi indice qui; copie in biblioteca), cap. 1, pp. 3-14. (versione preliminare in CERN Yellow Report 99-03).
• Per un resoconto pulito della dottrina officiale frequentista (soprattutto fra fisici) riguardo i "confidence intervals", vedi ad esempio G. Cowan, Statistical data analysis, soprattutto pp. 118-128. [ -> prob-stat_22 -> /CI/ :-) ]
   

Lezione 2 (22/1/09)

Test di ipotesi, loro significato(?) e fraintendimento: Probabilità delle ipotesi Vs probabilità della variabile di test (-> significatività statistica). Esempi accademici (possibile errore dello studente e scherzo alla rivista scientifica) e di interesse publico (test dell'AIDS).
Dalle cause agli effetti ("the essential problem of the experimental method ", Poincaré): inferenza e incertezza. Probabilità degli effetti Vs probabilità delle cause (e dei valori veri). Esempio guida: problema delle 6 scatole: che scatola ho scelto? che pallina uscirà cosa succede dopo la prima estrazione (con reimmissione)? dov'è la probabilità?
Approccio falsificazionista e sua implementazione pratica mediante i test di ipotesi. Significato ed errata interpretazione dei p-value, con esempi di annunci di false scoperte dovuti a banali errori di logica (es `eventi di HERA', 'Higgs a LEP', etc.).
Riferimenti

• GdA, Bayesian reasoning in data analysis - A critical introduction, cap. 1.
• GdA, From Observations to Hypotheses: Probabilistic Reasoning Versus Falsificationism and its Statistical Variations, physics/0412148, pp. 1-9.
• GdA, "Quanto credere alle diverse ipotesi scientifiche alla luce delle osservazioni sperimentali?", Incontro con insegnanti presso i LNF, settembre 2002 (con lucidi e video).
• Wikipedia, P-Value [vedi soprattutto 'Frequent misunderstandings' e l'articolo "Historical background on the widespread confusion of the p-value: a major educational failure" di R. Hubbard e J.S. Armstrong, ivi citato (copia locale: ps e pdf)].
• R. Hubbard and M.J. Bayarri, Confusion over measures of evidence (p's) versus errors (α's) in classical statistical testing, American Statistician, 57 (2003) 171-178.
• A. Palma, Frequentistic approaches in physics: Fisher, Neyman-Pearson and beyond (Presentazione di esame per questo corso di dottorato): pdf e ppt.
• Alcuni esempi di claim di scoperte basati su p-values (dopo alcuni anni alcuni siti non sono più raggiungibili...):
  • "The joint distribution has a probability of less than 1% to come from Standard Model": HERA events.
  • "La probabilità che gli eventi osservati siano una fluttuazione statistica è inferiore all'1%": comunicato INFN su eventi di HERA.
    [ -> "Il quark presto detronizzato da una nuova particella": un esempio di reazione (corretta) della stampa ]
  • "'It is a 2.6 sigma effect,' he told PhysicsWeb, 'so there's still a 6 in 1000 chance that what we are seeing are background events, rather than the Higgs.'": Higgs boson on the horizon.
  • "The experimenters reported a three-sigma discrepancy in sin2qW, which translates to a 99.75 percent probability that the neutrinos are not behaving like other particles": Neutrino Measurement Surprises Fermilab Physicists.

Lezione 3 (11/2/09)

Introduzione 'maieutica' a ragionamenti in condizione di incertezza (dadi, monete, previsioni meteo, conteggi osservati su rivelatori, etc.): valutazioni di "probabilità" (da meglio definire) nei vari casi.
Paradosso delle due buste di importi ignoti, dei quali si sa solo che uno è multiplo dell'altro.
Problema delle sei scatole (esempio guida): quale scatola ho estratto? Che colore osserverò? Cosa cambia dopo una o più estrazioni (con reintroduzione)? Dov'è la probabilità?
Paradosso di Ellsberg: scelta fra scatola con 5 palline bianche e 5 nere e scatola con proporzione ignota di bianche e nere (una delle `sei scatole')..
Probabilità secondo Hume.
Impossibilità di valutare f(μ|x) mediante puri ragionamenti di simmetria o mediante frequenze: -> inversione di probabilità. Cos'è la probabilità? Definizioni combinatoria, frequentista e soggettiva. Circolarità delle definizioni combinatorie e frequentiste.
Riferimenti

• GdA, Bayesian reasoning in data analysis - A critical introduction, par. 2.1, 2.2, 3.1, 3.2.
• D. Hume, An enquiry concerning human understanding (pdf qui), Secs. 46-47.
• GdA, Probabilità e incertezze di misura (vedi qui), problemi 33-36 a pag. 46 (parte 1).
   

Lezione 4 (12/2/07)

Probabilità come grado di fiducia: schema di de Finetti su Enciclopedia Einaudi. Probabilità condizionata: concetto. Significato del termine "soggettivo". Problemi delle tre scatole (o carte). Probabilità secondo Scroedinger (1947). Dipendenza della probabilità dallo stato di informazione. Differenza fra concetto di probabilità e sue regole di valutazione. Ruolo unificatore della probabilità Regole di base della probabilità ("assiomi di Kolmogorov" + "formula della probabilità condizionate") ottenute da: scommessa coerente (de Finetti-Ramsey); consistenza logica (Cox-Jaynes); calibrazione su eventi sui quali è possibile usare argomenti di simmetria (Lindley).
Confidenza espressa in termini di probabilità legata alla scommessa confrontata con i cosidetti "upper/lower" confidence limits: massa di saturno di Laplace e limite inferiore sulla massa dell'Higgs a LEP.
Ruolo ipotetico della scommessa. Distinzione fra soggettività e arbitrarietà. Recupero della regola di valutazione combinatoria. Probabilità e frequenza. Ruolo del calcolo combinatorio nella teoria della probabilità. Eventi, proposizioni e insiemi. Proprietà delle operazioni fra eventi/proposizioni e insiemi. Partizione finita e decomposizione della probabilità. Concetto di evento condizionato e significato della "formula della probabilità condizionata". Proprietà principali del calcolo di probabilitaà di eventi/proposizioni. Partizione finita e decomposizione della probabilità (legge delle alternative o formula di disintegrazione, o anche "delle probabilità totali).

Riferimenti

• E. Schroedinger, The foundation of the theory of probability - I, Proc. R. Irish Acad. 51A (1947) 51; reprinted in Collected papers Vol. 1 (Vienna 1984: Austrian Academy of Science) 463.
• B. de Finetti, voce Probabilità dell'Enciclopedia Einaudi, 1980.
• GdA, Bayesian reasoning in data analysis - A critical introduction, par. 3.2-3.4, 3.5.1-3.5.2, 10.1,10.2, pp. 224-225.
• GdA, CERN Academic Training, febbraio 2005, terza lezione, pp. 1-10, 24 (per pagina si intende la numerazione in basso a destra sui lucidi e non la numerazione delle pagine del file pdf).
• GdA, Bayesian Reasoning versus Conventional Statistics in High Energy Physics, MaxEnt98, physics/9811046.

Lezione 5 (18/2/07)

Problema dei tre prigionieri (analogo delle tre scatole).
Discussione su altre possibili obiezioni. In particolare: non arbitrarietà di affermazioni probabilistiche basate sulla coerenza e arbitrarietà di metodi convenzionali; grado di fiducia (cosa si crede) diverso da grado di convenienza (cosa piacerebbe accadesse) e da pura immaginazione; "oggettivià" e uso di "credenze" in fisica; "probabilità fisica". Le diverse faccie della probabilità: belief <--> chance (or propensity): Lewis' "Principal Principle".
Le quattro regole di base della probabilità (i tre `assiomi' più la formula `della probabilità condizionata') ricavate dalla condizione di coerenza.
Commenti sul significato di probabilità condizionata.
Uso delle formula simmetrica di aggiornamento della probabilità [P(H|E,I)/P(H|I)=P(E|H,I)/P(H,I)]: problema delle sei scatole con cinque palline B/N; problemi delle tre scatole.

Numeri incerti (aleatori) discreti e funzioni di probabilità. Esempi di costruzione di funzioni di variabili casuali dalle regole di base del calcolo delle probabilità. Propietà delle funzioni di probabilità. Funzione cumulativa e sue proprietà.
Cenni sui metodi di Monte Carlo ('branching' elementari, 'hit/miss' e inversione della cumulativa).
Processo di Bernoulli. Problema dell'ubriaco.

Riferimenti

• R. Scozzafava, Incertezza e probabilità (Zanichelli), 1.1-1.16.
• GdA, Bayesian reasoning in data analysis - A critical introduction (vedi qui), par. 10.3, 10.4,
• GdA, CERN Academic Training, febbraio 2005, terza lezione, pp. 11-29.
• GdA, Role and meaning of subjective probability: some comments on common misconceptions, MaxEnt2000, physics/0010064.
• Stanford Encyclopedia of Philosophy: Interpretation of probability.
• D. Lewis, A Subjectivist's Guide to Objective Chance. In Richard C. Jeffrey (ed.), Studies in Inductive Logic and Probability, Vol. II. Berkeley: University of Berkeley Press, 263-293. Reprinted with Postscripts in David Lewis (1986), Philosophical Papers. Vol. II. Oxford: Oxford University Press, 83-132. (versione pdf on line, e copia locale).
• GdA, Probabilità e incertezza di misura, Dispense del Dip. di Fisica (vedi qui), Parte 1, Capp. 1-4.
   

Lezione 6 (19/2/07)

Indipendenza logica e indipendenza stocastica.
Costituenti. Incompatibilità e indipendenza.
Attenzione alle sottigliezze dell'indipendenza stocastica (non strettamente legata a indipendenza fisica, ma piuttosto ai valori di probabilità non necessariamente transitiva): esempi

• Scatole con palline.
  1. Scatola con palline W, R e B equiprobabili. Dati E₁ = W .or. R ed E₂ = W .or. B (ove '.or.' sta per l'usuale simbolo di somma logica), calcolare se E₁ ed E₂ sono stocasticamente indipendenti o no.
  2. Idem, ma con palline W, R, B e Y.
• Mazzo di carte da poker con 52 carte, truccato (due Regine di quadri e nessuna Regina di fiore). Dati i tre eventi A = "Regina", B = "Rosso" (ovvero quadri o cuori) e C = "Cuori", valutare se sono stocasticamente indipendenti le seguenti coppie: A e B, B e C, A e C.

Eventi correlati positivamente e negativamente (con applicazione all'esempio delle sei scatole).
Ancora su metodi di MC: hit/miss e inversione della cumulativa. Valutazione di integrali con tecniche di campionamento e applicazione alla valutazione di pi greco.
Ancora su processo elementare di Bernoulli, distribuzione geometrica, binomiale e di Pascal.
Sintesi di distribuzioni di probabilità mediante opportuni parametri [convenzionali! - la nostra incertezza è completamente descritta da f(x)]: moda, mediana, 'baricentro' (media, valore atteso); intervallo di certezza; intervallo di probabilit`, momento di inerzia della distribuzione (varianza), deviazione standard.
Valore atteso come previsione (probabilistica) di un numero aleatorio e deviazione standard come incertezza (standard) di previsione.
Previsione, incertezza di previsione e incertezza di previsione relativa ('coefficiente di variazione') di geometrica, binomiale e poissoniana (quest'ultima introdotta ad hoc). Relazione formale fra binomiale e poissoniana.
Proprietà di valore atteso e varianza sotto trasformazioni lineari delle variabili. Generatore di numeri aleatori con probabilità secondo la distribuzione geometrica.
Quanto credere alla realizzazione della variabile casuale nell'intervallo di +- 1σ intorno alla previsione?
Introduzione al linguaggio R e al suo utilizzo ai fini del corso.

Riferimenti

• R. Scozzafava, Incertezza e probabilità (Zanichelli), 1.33 (su indipenza logico/stocastica).
• GdA, CERN Academic Training, febbraio 2005, terza lezione, pp. 30-40.
• GdA, Probabilità e incertezza di misura, Dispense del Dip. di Fisica (vedi qui), Parte 2, Cap. 6.
• N. Metropolis, The beginning of the Monte Carlo method,
  appeared in the Special Issue of Los Alamos Science (nr. 15, 1987) in memory of Stan Ulam.
• GdA, Introduzione al linguaggio R
  [inclusa geometrica.R, contenente anche rgeom1(), discussa a lezione.]