



Next: Correzione per errori sistematici
Up: Fattori di influenza non
Previous: Fattori di influenza non
Indice
Supponiamo di avere uno strumento le cui letture dipendono
da una costante di calibrazione che determina la lo zero
dello strumento (``offset''). Se lo strumento è stato calibrato
al meglio, crediamo che lo zero nominale corrisponderà conlo
zero vero, ma non ne possiamo essere assolutamente certi, in quanto
il processo stesso di calibrazione è soggetto ad incertezze.
Chiamiamo lo zero vero 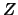 e modellizziamo la nostra incertezza su di esso
con una gaussiana di valore medio zero e deviazione standard
e modellizziamo la nostra incertezza su di esso
con una gaussiana di valore medio zero e deviazione standard
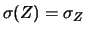 , ovvero
E
, ovvero
E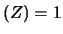 e
e
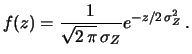 :
:
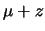 |
(11.31) |
Benché crediamo che la risposta dello strumento può essere descritta
da una gaussiana,
essa lo sarà non intorno a  , bensì intorno a
, bensì intorno a 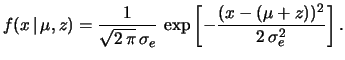 ,
ovvero la verosimiglianza sarà
,
ovvero la verosimiglianza sarà
![$\displaystyle f(x\,\vert\,\mu,z)= \frac{1}{\sqrt{2\,\pi}\,\sigma_e} \,\exp{\left[-\frac{(x-(\mu+z))^2}{2\,\sigma_e^2}\right]}\,.$](img3321.png) |
(11.32) |
Come prior vaga per  continuiamo ad utilizzare la distribuzione
uniforme. Otteniamo che l'inferenza condizionata ai possibili valori
di
continuiamo ad utilizzare la distribuzione
uniforme. Otteniamo che l'inferenza condizionata ai possibili valori
di 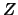 è data da
è data da
![$\displaystyle f(\mu\,\vert\,x,z)= \frac{1}{\sqrt{2\,\pi}\,\sigma_e} \,\exp{\left[-\frac{(\mu-(x+z))^2}{2\,\sigma_e^2}\right]}\,.$](img3322.png) |
(11.33) |
Applicando la formula generale (11.30) al nostro
caso particolare otteniamo
![$\displaystyle f(\mu\,\vert\,x)= \int_{-\infty}^{+\infty}\! \frac{1}{\sqrt{2\,\p...
...{2\,\pi}\,\sigma_Z} \exp{\left[-\frac{z^2}{2\,\sigma_Z^2}\right]} \,\rm {d}z\,,$](img3323.png) |
(11.34) |
ottenendo11.6
![$\displaystyle f(\mu\,\vert\,x) = \frac{1}{\sqrt{2\,\pi}\,\sqrt{\sigma_e^2+\sigma_Z^2}} \,\exp{\left[-\frac{(\mu-x)^2} {2\,(\sigma_e^2+\sigma_Z^2)}\right]}\,,$](img3325.png) |
(11.35) |
da cui segue la previsione
Il valore atteso di  è ancora
è ancora  , ma l'incertezza aumenta,
come effetto dell'incertezza sulla costante di calibrazione.
L'incertezza su
, ma l'incertezza aumenta,
come effetto dell'incertezza sulla costante di calibrazione.
L'incertezza su  dovuta ai soli effetti casuali
si combina in quadratura con quella di calibrazione
della costante di zero.
dovuta ai soli effetti casuali
si combina in quadratura con quella di calibrazione
della costante di zero.
È interesante vedere cosa succede se, invece di una singola misura
abbiamo una singola osservazione equivalente (nel senso del
paragrafo 11.2), costituita dalla media
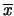 di
di  osservazioni individuali.
Avremo allora
osservazioni individuali.
Avremo allora
Questo ci insegna che, anche effettuato un ``numero infinito'' di misure,
l'incertezza non si annullerà mai, in quanto, ad un certo livello,
interverranno sempre effetti sistematici che saranno dominanti
ai fini dell'incertezza. La (11.39) ci insegna anche
come pianificare l'esperimento per bilanciare correttamente numero
di osservazioni e controllo della sistematica. Si noti comunque
che le cose possono cambiare, se il risultato va opportunamente combinato.
Ad esempio se misuriamo con lo stesso strumento 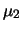 e
e 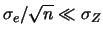 e
siamo poi interessati alla loro differenza, ha senso arrivare
anche a
e
siamo poi interessati alla loro differenza, ha senso arrivare
anche a
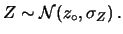 . Di questo parleremo
nel paragrafo 11.6.3.
. Di questo parleremo
nel paragrafo 11.6.3.




Next: Correzione per errori sistematici
Up: Fattori di influenza non
Previous: Fattori di influenza non
Indice
Giulio D'Agostini
2001-04-02
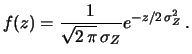 :
:
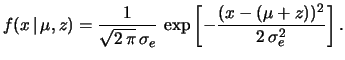 ,
ovvero la verosimiglianza sarà
,
ovvero la verosimiglianza sarà
![$\displaystyle f(x\,\vert\,\mu,z)= \frac{1}{\sqrt{2\,\pi}\,\sigma_e} \,\exp{\left[-\frac{(x-(\mu+z))^2}{2\,\sigma_e^2}\right]}\,.$](img3321.png)
![$\displaystyle f(\mu\,\vert\,x,z)= \frac{1}{\sqrt{2\,\pi}\,\sigma_e} \,\exp{\left[-\frac{(\mu-(x+z))^2}{2\,\sigma_e^2}\right]}\,.$](img3322.png)
![$\displaystyle f(\mu\,\vert\,x)= \int_{-\infty}^{+\infty}\! \frac{1}{\sqrt{2\,\p...
...{2\,\pi}\,\sigma_Z} \exp{\left[-\frac{z^2}{2\,\sigma_Z^2}\right]} \,\rm {d}z\,,$](img3323.png)
![$\displaystyle f(\mu\,\vert\,x) = \frac{1}{\sqrt{2\,\pi}\,\sqrt{\sigma_e^2+\sigma_Z^2}} \,\exp{\left[-\frac{(\mu-x)^2} {2\,(\sigma_e^2+\sigma_Z^2)}\right]}\,,$](img3325.png)
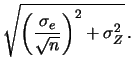
![]() di
di ![]() osservazioni individuali.
Avremo allora
osservazioni individuali.
Avremo allora