



Next: Variabili casuali indipendenti
Up: Estensione dei teoremi sulla
Previous: Estensione dei teoremi sulla
Indice
In analogia alla probabilità condizionata esistono
le distribuzioni di probabilità condizionate, nel senso
che 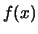 può essere subordinata alla conoscenza
che
può essere subordinata alla conoscenza
che  sia uguale a
sia uguale a 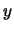 , ovvero
, ovvero
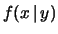 .
Essa è indicata con
ed è funzione soltanto di
.
Essa è indicata con
ed è funzione soltanto di  , mentre
, mentre 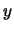 svolge, per così
dire, il ruolo di
parametro. Quindi esistono tante diverse
svolge, per così
dire, il ruolo di
parametro. Quindi esistono tante diverse
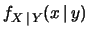 quanti sono i possibili valori di
quanti sono i possibili valori di  , infiniti nel caso che
, infiniti nel caso che
 sia una variabile continua.
sia una variabile continua.
Come detto nel paragrafo 7.16, l'estensione
al caso discreto è immediata. Vediamo come ci si comporta
per il caso continuo.
Ricordiamo la formula che lega probabilità condizionata alla congiunta
(vedi paragrafo 4.6):
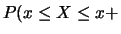 |
(9.3) |
Nel caso di variabile casuale continua
possiamo scrivere in perfetta analogia:
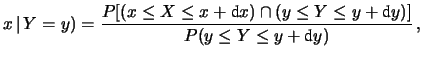 d d![$\displaystyle x\,\vert\, Y = y) = \frac{P[(x\le X \le x + \mbox{d}x) \cap (y\le Y\le y+\mbox{d}y)]} {P(y\le Y\le y+\mbox{d}y)}\, ,$](img2202.png) |
(9.4) |
con
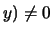 d
d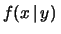 .
Passando alle funzioni densità di probabilità si ha
.
Passando alle funzioni densità di probabilità si ha
da cui
con 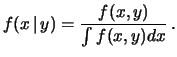 . Si ricorda che, come visto per
la (9.3), neanche la
(9.5) definisce
la distribuzione condizionata.
In particolare,
. Si ricorda che, come visto per
la (9.3), neanche la
(9.5) definisce
la distribuzione condizionata.
In particolare,
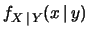 può essere valutata senza
che sia nota (o abbia importanza) la funzione congiunta
può essere valutata senza
che sia nota (o abbia importanza) la funzione congiunta 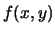 (vedi discussioni ai paragrafi
4.4
4.6). È comunque chiaro che,
qualora invece la
(vedi discussioni ai paragrafi
4.4
4.6). È comunque chiaro che,
qualora invece la 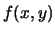 sia assegnata, essa contiene l'informazione
più completa sullo stato di incertezza di
sia assegnata, essa contiene l'informazione
più completa sullo stato di incertezza di  e di
e di  , in quanto
da essa è possibile ricavarsi le marginali e le condizionate,
ad esempio:
, in quanto
da essa è possibile ricavarsi le marginali e le condizionate,
ad esempio:
Si noti come la formula (9.5) non
dipenda dal fatto che le 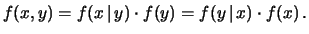 siano
probabilità o densità di probabilità, ovvero la formula
è indipendentemente dal tipo di variabili. Inoltre,
per simmetria, si ha
siano
probabilità o densità di probabilità, ovvero la formula
è indipendentemente dal tipo di variabili. Inoltre,
per simmetria, si ha
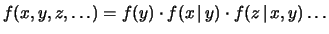 |
(9.6) |
Così pure, in modo analogo alla (4.22),
si ha, nel caso di molte variabili:




Next: Variabili casuali indipendenti
Up: Estensione dei teoremi sulla
Previous: Estensione dei teoremi sulla
Indice
Giulio D'Agostini
2001-04-02
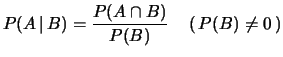
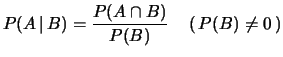
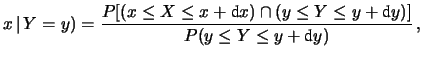 d
d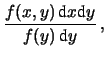 d
d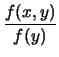
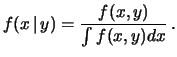 . Si ricorda che, come visto per
la (9.3), neanche la
(9.5) definisce
la distribuzione condizionata.
In particolare,
. Si ricorda che, come visto per
la (9.3), neanche la
(9.5) definisce
la distribuzione condizionata.
In particolare,
![]() siano
probabilità o densità di probabilità, ovvero la formula
è indipendentemente dal tipo di variabili. Inoltre,
per simmetria, si ha
siano
probabilità o densità di probabilità, ovvero la formula
è indipendentemente dal tipo di variabili. Inoltre,
per simmetria, si ha