This report introduces general ideas and some
basic methods of the Bayesian probability theory
applied to physics measurements.
Our aim is to make the reader familiar, through examples
rather than rigorous formalism, with concepts such as:
model comparison
(including the automatic
Ockham's Razor filter provided
by the Bayesian approach); parametric inference;
quantification of the uncertainty
about the value of physical quantities, also taking
into account systematic effects; role of marginalization;
posterior characterization;
predictive distributions;
hierarchical modelling and hyperparameters;
Gaussian approximation of the posterior
and recovery of conventional methods, especially maximum likelihood
and chi-square fits under well defined conditions;
conjugate priors, transformation invariance and maximum
entropy motivated priors; Monte Carlo estimates of expectation,
including a short introduction to Markov Chain Monte Carlo
methods.
1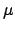 and
and 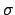 of a Gaussian
of a Gaussian